El Sistema del Mundo

Libro

Del Sistema del Mundo

1. Que los cielos son fluidos

Fue muy antigua la opinión de los filósofos de que las fijas permanecían inmóviles en las regiones más altas del mundo, de que los planetas, más abajo, giraban en torno al Sol, de que, de modo similar, la Tierra se movía con un curso anual, mientras sobre el propio eje lo hacía con giro diurno, de que el Sol, o foco del universo, reposaba en el centro de todos ellos. Así habían opinado en otro tiempo Filolao, Aristarco de Samos, Platón en su edad madura, multitud de Pitagóricos,[2] y Anaximandro más antiguo que ellos, lo mismo que Numa Pompilio aquel sabio rey de los Romanos. Arquímedes en el Arenario. Aristarco, en lib. 2 del cielo. Plutarco en el lib. 3 de los Placita Philosoforum y también Numa. Este, como símbolo del orbe esférico y del fuego solar en el centro, erigió un templo a Vesta, de forma circular, y ordenó que se mantuviese un fuego perpetuo en el centro del mismo. Es verosímil empero, que esta opinión se propagase a partir de los egipcios, antiquísimos observadores de los astros. Así pues, de ellos y de sus vecinos parece que pasó a los griegos, gente más filológica que filosófica, toda la filosofía más antigua a la vez que más sensata; y los sagrados misterios de Vesta, superando el conocimiento del vulgo gustan al ingenio de los egipcios, pintores de ritos sagrados y jeroglíficos. Pero después Anaxágoras, Demócrito, y muchos otros enseñaron que la Tierra permanece inmóvil en el centro del mundo, y que los astros todos se mueven hacia el ocaso unos más rápidamente, otros más lentamente y esto en espacios totalmente libres. Después fueron introducidas las esferas sólidas por Eudoxo, Calipo y Aristóteles, al ir decayendo poco a poco la filosofía inicialmente recibida y al prevalecer poco a poco las nuevas formulaciones de los Griegos. Difícilmente se compaginan con estas esferas los fenómenos de los Cometas. Los Caldeos, gente muy experta en temas astronómicos, consideraron como estrellas errantes a dichos Cometas,[3] computados desde antiguo por muchos entre los cuerpos celestes: como si una vez en cada revolución, descendiendo a las partes inferiores de órbitas muy excéntricas se nos mostrasen observando por veces. Después la hipótesis de las órbitas sólidas los redujo necesariamente a las regiones sublunares; y debido a nuevas observaciones de los astrónomos, restituidos a los cielos supralunares, aquellas esferas se quebraron y fueron desalojadas del éter.

2. El principio del movimiento circular en los espacios libres

No sabemos con qué vínculos los antiguos retenían a los planetas en los espacios libres, y enseñaron que, apartados continuamente de la trayectoria rectilínea, giran regularmente en sus órbitas. Creo que para explicar esto se inventaron las esferas sólidas. Los filósofos más recientes o piensan que son los vórtices, como Kepler o Descartes, o algún otro impulso o principio de atracción, como Borelli, Hooke y otros de entre los nuestros. Por la Ley primera del movimiento es absolutamente cierto que se requiere alguna fuerza. Es nuestro propósito elucidar su cantidad y propiedades e investigar matemáticamente los efectos en los cuerpos en movimiento; por tanto, para no determinar su especie de manera hipotética, la hemos denominado centrípeta con un nombre genético, por cuanto tiende a un centro o también, tomando el nombre del centro, circunsolar a la que tiende al Sol; circunterrestre a la que tiende la Tierra; circunjovial a la que tiende a Júpiter, y así en los demás.

3. Efectos de las fuerzas centrípetas

De los movimientos de los proyectiles se comprende que los planetas pueden ser retenidos en órbitas ciertas mediante fuerzas centrípetas. Una piedra lanzada, sometida a la acción de su gravedad, se desvía de la trayectoria rectilínea y, describiendo una curva en el aire, cae al fin al suelo; si se lanzase con mayor velocidad, llegará más lejos. Aumentando la velocidad, podría lograrse que describiera un arco de una milla, dos, cinco, cien, mil; y por fin, al ir más allá de los límites de la Tierra, que no cayese ya en el suelo.

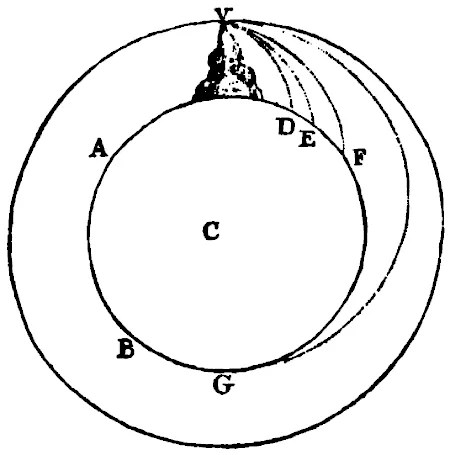
Sea AFB la superficie de la Tierra; sea C su centro; y VD, VE, VF las líneas curvas descritas por un proyectil lanzado desde el vértice V de un monte muy alto, líneas paralelas a la línea del horizonte, resultado de lanzamientos sucesivos, aumentados cada uno con los correspondientes grados de velocidad. Y para que no intervenga la resistencia del aire, que apenas en nada retrasa los movimientos celestes, imaginemos que se ha suprimido o que por lo menos no ofrece resistencia alguna. Y por la misma razón por la que el cuerpo con menor velocidad describe el arco menor VD, y el de velocidad mayor describe el arco mayor VE, y si se aumenta la velocidad llega aún más lejos hasta F, y aún más lejos hasta G; finalmente este mismo, si se le aumenta la velocidad continuamente, sobrepasará al monte desde donde fue lanzado. Puesto que el área descrita por el radio que le unía al centro de la tierra será (por la Prop. I del Lb. I Princp. Math.) proporcional al tiempo, su velocidad al regresar al monte no será menor que al principio: y manteniendo la velocidad puede girar así muchas veces por la misma ley. Imaginemos ahora que los cuerpos son lanzados según las líneas del horizonte desde puntos más altos; pongamos desde lugares de cinco, diez, cien, mil millas o más de altitud, o hasta incluso semidiámetros de la Tierra; y según la distinta velocidad de los cuerpos, y según la diferente gravedad ejercida en cada región describirán arcos Terrestres ya concéntricos, ya de excentricidades diversas; y en estas trayectorias los cuerpos recorrerán los cielos de modo semejante al de los planetas.

4. Certeza del argumento

Y del mismo modo que de la caída de la piedra lanzada se deduce demostrativamente que gravita, tampoco es indicio menos cierto de gravedad aquella continua desviación de los proyectiles hacia la tierra; del mismo modo todo desvío del camino recto de todos los cuerpos en movimiento en espacios libres, y la continua inclinación hacia cualquier lugar, es indicio seguro de que existe alguna fuerza por la que los cuerpos son afectados por doquier hacia ese lugar. Y puesto que una vez admitida la gravedad es necesario que todos los cuerpos tiendan en la Tierra hacia lugares más bajos; y por lo mismo, o bien caen en línea recta si se los suelta desde el estado de reposo, o bien, si se los lanza oblicuamente, se desvían continuamente de la trayectoria recta hacia la Tierra; así también, concedido que una fuerza tiende a un centro, no es menos necesario que todos los cuerpos sobre los que se ejerce dicha fuerza o bien desciendan rectamente hacia ese centro, o bien, si se mueven oblicuamente, se dirijan perpetuamente hacia el centro desviándose del camino recto. Pero la razón para deducir las fuerzas de los movimientos y los movimientos de las fuerzas se expuso extensamente en los Libros del Movimiento.

5. Las fuerzas centrípetas tienden a los centros de cada planeta

Deduzco que las fuerzas centrípetas tienden hacia los cuerpos del Sol, de la Tierra y de los Planetas, del modo siguiente. La Luna gira en torno a nuestra Tierra, y con radios trazados al centro de la misma Tierra, describe áreas proporcionales a los tiempos muy aproximadamente. Esto resulta totalmente cierto de la comparación de la velocidad de la Luna con sus diámetros aparentes: con un diámetro menor, cosa que arguye mayor distancia, el movimiento es más lento; con un diámetro mayor, más rápido. Los satélites de Júpiter giran en torno a este con movimientos mucho más regulares, describiendo círculos concéntricos a Júpiter con movimiento igual según lo que se ve. Lo mismo el compañero de Saturno se mueve en torno a este planeta con un movimiento bastante circular y constante, sin que se observe excentricidad apenas. Que Venus y Mercurio se mueven en torno al Sol se demuestra por sus fases lunares: al otro lado del Sol muestran su cara entera, a la altura del Sol, la mitad; a este lado del Sol, en forma curvada, pasando a veces por el disco del Sol. Venus ciertamente describe una órbita circular, concéntrica al Sol y con movimiento casi uniforme. En cambio Mercurio, con un movimiento más excéntrico, se acerca mucho al Sol y desde allí se aleja poco a poco; pero siempre es más veloz cuando está más cerca del Sol, lo que hace que, con un radio trazado al Sol, describa áreas proporcionales a los Tiempos. Por fin, que la Tierra en torno al Sol o el Sol en torno a la Tierra describen, con el radio que los une, áreas exactamente proporcionales a los tiempos, se demuestra a partir de la comparación del diámetro aparente del Sol con su movimiento aparente. Estos son los experimentos astronómicos: y a partir de estos (por las tres Proposiciones primeras del Libro Primero y sus Corolarios) se infiere que se dan fuerzas centrípetas, ya exactamente, ya sin error notable, tendentes a los centros de la Tierra, de Júpiter, de Saturno. Para Venus, Marte, y los planetas menores, al faltar los experimentos, valga el argumento por analogía.

6. Las fuerzas centrípetas decrecen en razón cuadrada de la distancia a los centros de los planetas

Del corolario sexto de la proposición cuarta se sigue que estas fuerzas decrecen en razón al cuadrado de las distancias desde el centro de un planeta cualquiera. Pues los períodos de tiempo de los Satélites de Júpiter se corresponden entre sí en proporción sesquiáltera a las distancias desde el centro de este planeta. Ya hace tiempo que se observó en ellos esta proporción; y tan exacta como es posible obtener por los sentidos me la dio a mí nuestro Flamsteed, quien midió muchas veces esta distancia por el Micrómetro y por medio de los eclipses de los satélites. Antes del descubrimiento del Micrómetro, Galileo, partiendo del satélite interior hacia el exterior, estableció que eran al semidiámetro de Júpiter como 6, 10, 16, 28 respectivamente; Simón Mario, 6, 10, 16, 26; Cassini, 5, 8, 13, 23, Borelli, más exactamente, 5, 8, 14, 24. Y después del descubrimiento del Micrómetro, Townley, 5,51; 8,78; 13,47; 24,72 y más exacto aún por los eclipses, 5,578; 8,876; 14,159; 24,903; pero los períodos de tiempo de los satélites según las observaciones de Flamsteed son de 1d 18h 28’36”; 3d 13h 17’54”; 7d 3h 59’36”; y 16d 18h 5’13”. Las distancias derivadas de esto son como los números 5,578, 8,878, 14,168, 24,968 que se corresponden bastante bien con las distancias obtenidas mediante observación y en los planetas circunsolares, Mercurio y Venus, tal proporción resulta exacta; al menos en la medida en que los astrónomos han establecido las dimensiones de las órbitas hasta ahora, mediante las observaciones mejor conocidas.

7. Los planetas superiores ciñen al Sol y con radios trazados hasta este describen áreas proporcionales a los tiempos.

Que Marte también gira en torno al Sol se demuestra por sus fases y por la proporción de sus diámetros aparentes, pues es seguro que gira alrededor del Sol debido a su fase llena junto a su conjunción con el Sol y sus fases ojivadas en los cuadrantes; y por cuanto su diámetro aparente sea cinco veces mayor en la oposición que en la conjunción con el Sol, y como su distancia a la Tierra sea recíprocamente proporcional a su diámetro aparente, dicha distancia será alrededor de cinco veces menor en la oposición que en la conjunción; pero la distancia de Marte al Sol será aproximadamente la misma, para ambos casos que su distancia en los cuadrantes, cuando se deduce de la fase ojivada. Y de igual modo que ciñe al Sol a una distancia prácticamente igual, mientras a la Tierra lo hace a distancia muy desigual, también, trazando un radio al Sol, describe un área bastante regular; mientras que con el trazado a la Tierra, ahora es más veloz, después estacionario, más tarde retrógrado. Que Júpiter es superior a Marte y que ciñe también al Sol con un movimiento bastante regular en cuanto a la distancia y a la descripción de área lo deduzco del modo siguiente. En cartas que me han sido entregadas ha escrito el Ilustre Flamsteed que todos los eclipses del satélite interior que ha conocido y hasta ahora observado con precisión están acorde con su teoría sin error de tiempo de dos minutos primeros; el exterior no se desvía mucho más, el pre-exterior, apenas se desvía tres veces más y el inmediato al interior mucho más; pero en todo caso se desvía menos de sus cálculos que lo que suele hacer la Luna respecto a las tablas comunes: él sin embargo, ha calculado los eclipses únicamente por los movimientos medios de los satélites y por la ecuación de la luz descubierta por Römer. Supongamos pues que la teoría se desvía, respecto al movimiento del satélite exterior observado hasta ahora menos que un error de dos minutos primeros: entonces el período completo de 16d 18h 5’13”, será al tiempo de 2’ como todo el círculo de 360 grados al arco de 1’48”.[4] Por tanto el error de cálculo de Flamsteed, reducido a la órbita del Satélite, será menor que 1’48”, esto es, la longitud del satélite considerado desde el centro de Júpiter se podrá determinar sin error de 1’48”. Pero dicha longitud, mientras el satélite discurre por el centro de la zona de sombra, es la misma que la longitud heliocéntrica de Júpiter y, por tanto, la hipótesis que sostiene Flamsteed, a saber la de Kepler-Copémico, ya de por sí correcta (respecto al movimiento de Júpiter), muestra correctamente dicha longitud sin error de 1’48”. Con esta longitud y la siempre bien conocida longitud geocéntrica, se determina la distancia de Júpiter al Sol, que por lo demás siempre es la que proporciona esta hipótesis. Puesto que aquel error máximo de 1’48” en la longitud heliocéntrica es casi insensible y se ha de despreciar; e incluso puede proceder de una excentricidad desconocida del Satélite. Una vez definidas correctamente la longitud y la distancia, es preciso que Júpiter con un radio trazado hasta el Sol, describa áreas según la ley que esta hipótesis requiere, y, por tanto, proporcionales al tiempo. Lo mismo podría deducirse respecto a Saturno a partir de su vecino por medio de las observaciones de Huygens y Halley; aunque sea de desear que la serie continuada de las observaciones lleven a una confirmación del tema y a un cálculo más preciso.

8. La fuerza por la que se rigen los planetas superiores no se dirige a la Tierra. Se dirige al Sol

Por consiguiente, si alguien contemplase a Júpiter desde el Sol, nunca lo vería retrocediendo, ni estacionario, como se ve desde la Tierra, sino que lo vería siempre progresando con un movimiento bastante uniforme. De la suma desigualdad del movimiento aparente geocéntrico se deduce, por el corolario cuarto de la proposición tercera, que la fuerza por la que Júpiter es obligado a apartarse del movimiento rectilíneo y girar en una órbita, no se dirige al centro de la Tierra, y también vale el mismo argumento para Marte y Saturno. Hay que buscar, por las Prop. II y III y los corolarios de esta, otro centro de estas fuerzas, en torno al cual, con radios entrecruzados, se describa un área igual a la que se ha descrito: y ya se ha probado que tal es el Sol para Marte y también para Saturno y para Júpiter además muy exactamente. Puede imaginarse que el Sol y los Planetas son impelidos por otra fuerza cualquiera constante y que actúa según líneas paralelas. Pero con tal fuerza no cambiará el lugar de los planetas entre sí, por el Corolario 6 de las Leyes; no se producirá ningún efecto observable; nosotros tratamos, en cambio, de causas de fenómenos observables. Rechacemos, pues, toda fuerza de este tipo por carecer de fundamento y que en nada afecta a los fenómenos celestes; toda la fuerza restante que actúe sobre el astro Júpiter tiende, por el Corolario Primero de la Proposición Tercera, al centro del Sol.

9. La fuerza circumsolar decrece en todo el ámbito planetario proporcionalmente al cuadrado de las distancias al Sol

Las distancias de los planetas al Sol vienen a ser las mismas, tanto si, con Tycho, colocamos a la Tierra en el centro del sistema, como si, con Copérnico, a quien colocamos es al Sol: y ya hemos probado que dichas distancias son verdaderas en el caso de Júpiter. Para su determinación fue excelente la contribución de Kepler y Bullialdo: y en consecuencia sus Tablas concuerdan muy bien con los ciclos. Así pues los cubos de estas distancias en todos los planetas, quiero decir en Júpiter y Marte, Saturno y la Tierra, lo mismo que en Venus y Mercurio, son como los cuadrados de los tiempos periódicos; y por tanto, por el Corolario 6 de la Prop. IV, la fuerza centrípeta circumsolar decrece por todo el ámbito planetario celeste, según el cuadrado de las distancias al Sol. Para estudiar esta proporción han de tomarse las distancias medias, o los semiejes transversales de las órbitas (por la Prop. XV) y despreciar las minucias que, al determinar las órbitas, pudieran originarse de errores inapreciables de las observaciones, o que habría que atribuir a causas de ulterior determinación. De este modo siempre se llegará exactamente a la proporción preestablecida, puesto que las distancias obtenidas a partir de las observaciones de los astrónomos entre Saturno, Júpiter, Marte, Tierra, Venus y Mercurio y el Sol estarían entre sí, de acuerdo con el cómputo de Kepler, como los números 951 000, 519 650, 152 350, 100 000, 73 400, y, según el cómputo de Bullialdo, como los números 954 198, 522 520, 152 350, 100 000, 72 398, 38 585; y dichas distancias obtenidas a partir de los tiempos periódicos son como los números 953 806, 520 116, 152 399, 100 000, 72 388, 38 710. Las distancias de Kepler y Bullialdo, apenas difieren sensiblemente y donde difieren en mayor medida, comprenden en medio a las distancias obtenidas de los tiempos periódicos.

10. La fuerza circumterrestre decrece en razón del cuadrado de la distancia a la Tierra. Se prueba bajo la hipótesis de que la Tierra está en reposo

Así deduzco que la fuerza circumterrestre decrece también en proporción al cuadrado de las distancias. La distancia media de la Luna al Centro de la Tierra es según Ptolomeo, Kepler en las Efemérides, Bullialdo, Hewelcke y Riccioli de 59 semidiámetros terrestres; según Flamsteed de 58; según Vendelin de 60, según Copérnico de 60; según Kircher de 62; según Tycho de 56: Pero Tycho y cuantos siguieron sus tablas de refracción, al considerar las refracciones del Sol y de la Luna mayores que las de las estrellas fijas, totalmente en contra de la naturaleza de la luz, y esto en casi cuatro o cinco segundos, aumentaron en otro tanto la paralaje de la Luna; esto es casi en la doceava o décima quinta parte de toda la paralaje. Corrijamos este error y resultará una distancia de casi 61 semidiámetros terrestres; casi lo asignado por los demás. Asumamos como distancia media la de sesenta semidiámetros; el período lunar respecto a las estrellas fijas se completa en 27 días 7 horas y 43 minutos, como ha sido establecido por los astrónomos; por el Corolario Sexto de la Proposición cuarta, un cuerpo, que gire en nuestra atmósfera junto a la superficie de la Tierra en reposo, empujado por una fuerza centrípeta que fuese a la misma fuerza a la distancia de la Luna recíprocamente como el cuadrado de las distancias al Centro de la Tierra, esto es como 3600 a 1, suprimida la resistencia del aire, completaría una revolución en 1 hora 24 minutos 27 segundos. Supongamos que el perímetro terrestre es de 123 249 600 pies parisinos, como ha sido recientemente establecido por los medidores franceses, y dicho cuerpo, suprimido el movimiento rotatorio y bajo la acción de la misma fuerza centrípeta anterior, recorrería al caer 15 pies parisinos en el tiempo de un segundo. Se sigue esto del cálculo efectuado por la Proposición XXXVI, y concuerda con la experiencia. Pues realizados experimentos con péndulos y hecho el cálculo sobre ellos, Huygens ha demostrado que los cuerpos que caen en las inmediaciones de la Tierra empujados por esa fuerza centrípeta sea del tipo que sea, recorren 15 pies parisinos en el tiempo de un segundo.

11. Se prueba bajo la hipótesis de que la Tierra se mueve

Si se le concede movimiento a la Tierra, giren esta y la Luna en torno a un centro común de gravedad por el Cor. 4 de las Leyes y por la Prop. LVII. La Luna (por la Proposición LX) completará su órbita en el mismo tiempo periódico de 27 días, 7 horas, 43 minutos, con la misma fuerza circumterrestre disminuida proporcionalmente al cuadrado de la distancia, siendo el semidiámetro de esta órbita al semidiámetro de la anterior, esto es a 60 semidiámetros terrestres, como la suma de los cuerpos de la Tierra y de la Luna a (la raíz) primera de la media proporcional de los dos entre esta suma y el cuerpo de la Tierra; esto es, si suponemos que la Luna viene a ser por su diámetro medio aparente de 31 minutos como la cuarenta y dosava parte de la Tierra, como 43 a ; o como 128 a 127 aproximadamente; y por tanto el semidiámetro de esta órbita, esto es la distancia entre los centros de la Tierra y de la Luna, vendrá a ser de 60 semidiámetros terrestres, casi lo asignado por Copérnico, sin discrepancia con las observaciones de Tycho. A esta distancia es válida la proporción aquella del cuadrado en el decrecimiento de las fuerzas. El incremento de la órbita debido a la acción del Sol, lo he despreciado por ser insignificante; descontado este, nos queda la verdadera distancia de casi 60 semidiámetros terrestres.

12. Se prueba el decrecimiento proporcional al cuadrado de las distancias a la Tierra y a los Planetas a partir de la excentricidad de los planetas y del lentísimo movimiento de los ábsides

Se confirma además esta proporción en el decrecimiento de las fuerzas a partir de la excentricidad de los planetas y de la lentitud de los movimientos absidales, pues (por los Corolarios de la Prop. XLV) está claro que con ninguna otra proporción todos los planetas circumsolares podrían, en cada revolución, descender una vez hasta la mínima distancia al Sol y ascender otra vez hasta la máxima distancia al Sol permaneciendo inmóviles los lugares de estas distancias. Un pequeño error en la proporción del cuadrado de las distancias produciría un notable movimiento de los ábsides en cada revolución, y enorme en muchas. Pero tal movimiento apenas resulta observable después de incontables revoluciones en las órbitas de los planetas circumsolares. Algunos astrónomos niegan todo movimiento; los demás no lo consideran mayor que el que fácilmente podría originarse de causas a asignar posteriormente, cosa de ninguna importancia en esta cuestión. Pero incluso el movimiento mucho mayor del Afelio lunar, que resulta de tres grados para cada revolución, puede despreciarse. Con este movimiento se demuestra que la fuerza circumterrestre decrece en una proporción no menor que el cuadrado de la distancia y mucho menor que el cubo; pues si la razón del cuadrado se hace variar paulatinamente hacia el cubo, el movimiento del Afelio aumenta hasta el infinito, hasta el punto de que con una variación muy pequeña se superara el movimiento del Afelio lunar. Se origina tal movimiento sumamente lento por la acción de la fuerza circumsolar, como se dirá después. Suprimiendo esta causa queda en reposo el apogeo de la Luna y se llega a la proporción del cuadrado.

13. Cantidad de las fuerzas terrestres respecto a cada planeta. La inmensa fuerza circumsolar

Establecida esta proporción, es ya posible comparar entre sí las fuerzas de los planetas. En la distancia media de Júpiter y la Tierra la elongación máxima desde el centro de Júpiter del satélite exterior es, según las observaciones de Flamsteed, de 18’13”. Y por tanto la distancia del satélite al Centro de Júpiter es a la distancia media de Júpiter al Centro del Sol, como 124 a 52 012, y a la distancia media de Venus al Centro del Sol como 124 a 7234. Por otra parte sus tiempos periódicos son de 16 y de 224 días. De aquí que por el Segundo Corolario de la Cuarta Proposición, dividiendo las distancias por los cuadrados de lo tiempos, se deduce que la fuerza, por la que el satélite es empujado hacia Júpiter, es a la fuerza por la que Venus es empujado hacia el Sol como 442 a 143: y restando la fuerza, por la que el satélite es empujado, según la razón del cuadrado, de la distancia 124 a 7234, resultará la fuerza circumjovial a la distancia de Venus al Sol respecto a la fuerza circumsolar por la que Venus es empujada, como 13 100 a 143 o también como 1 a 1100. Por tanto a distancias iguales la fuerza circumsolar es 1100 veces mayor que la circumjovial. Mediante un cálculo similar, a partir del tiempo periódico del satélite de Saturno de 15 días y 22 horas y una elongación máxima respecto al propio Saturno de 3’20” a distancia media de nosotros, deduzco que la distancia de este Satélite respecto al centro de Saturno es a la distancia de Venus al Sol como 92 a 7234; y de aquí que la fuerza absoluta circumsolar es 2360 veces mayor que la fuerza absoluta circumsaturnal.

14. Pequeña fuerza circumterrestre

Del movimiento regular heliocéntrico de Venus, Júpiter y otros planetas y del irregular movimiento geocéntrico de los mismos se desprende con claridad (por el Corolario 4 de la Prop. III) que la fuerza circumterrestre comparada con la circumsolar es muy pequeña. Riccioli y Vendelin intentaron determinar por separado la paralaje del Sol a partir de la dicotomía de la Luna observada por los telescopios, y la cifraron en no más de medio minuto. Kepler halló insensible, a partir de las observaciones de Tycho y de las suyas propias la paralaje de Marte acrónico que es mucho mayor. Flamsteed lo abordó con el micrómetro, y eso en el perigeo de Marte, y nunca la encontró mayor de veinticinco segundos; de aquí concluyó que la paralaje solar sería a lo sumo de diez segundos. De donde se sigue que la distancia de la Luna a la Tierra no está en mayor proporción respecto a la distancia de la Tierra al Sol que 29 a 10 000, ni mayor respecto a la distancia de Venus al Sol que 29 a 7233. A partir de aquí y de los tiempos periódicos, según el método expuesto, se deducirá que la fuerza circumsolar absoluta será como mínimo 229 400 veces mayor que la fuerza absoluta circumterrestre. Si esto se conociese únicamente por medio de las observaciones de Riccioli y de Vendelin de que la paralaje es menor de medio minuto, se seguiría de ello que la fuerza absoluta circumsolar superaría a la circumterrestre 8500 veces.

15. Diámetros aparentes de los planetas

Mediante cálculos similares abordé la analogía entre fuerzas y masas planetarias; pero antes de exponer esto hay que determinar los diámetros aparentes de los planetas a sus distancias medias de la Tierra. Flamsteed midió con micrómetro el diámetro de Júpiter resultando 40” o 41” y el del anillo de Saturno de 50” y el del Sol de 31’13”. El diámetro del cuerpo de Saturno es al del anillo, según Huygens y Halley como 4 a 9, según Gallet como 4 a 10 y según Hooke (que utilizó un telescopio de sesenta pies) como 5 a 12. En razón de la media de 5 a 12 se colige un diámetro para el cuerpo de Saturno de casi 21”.

16. Corrección de los diámetros aparentes

Efectivamente estas son magnitudes aparentes, pero, por la desigual refrangibilidad de la luz, todos los puntos luminosos se dilatan en los telescopios y ocupan en el foco del objetivo de cristal un espacio circular de casi la cincuentava parte de la apertura del cristal; hasta tal punto que la luz en la periferia apenas o ni apenas se percibe; en cambio, en el centro, donde es más densa y afecta suficientemente a la vista, constituye un círculo luminoso y corresponde a la tercera o cuarta parte o como mucho a la quinta parte de la amplitud total.

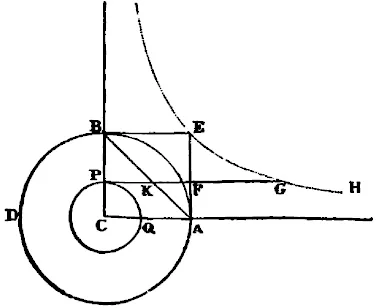
Sea ABD el círculo luminoso total; PQ el círculo menor iluminado con luz suficientemente perceptible; C el Centro de ambos; CA, CB los semidiámetros del círculo mayor que contienen el ángulo recto C; ACBE el cuadrado comprendido entre estos diámetros. AB su diagonal; EGH la hipérbola descrita con centro C y asíntotas CA, CB; PG una perpendicular a la propia CB levantada desde un punto cualquiera P, y que corta a la hipérbola en G y a las rectas AB, AE en K y F: y la densidad de la luz será en un punto cualquiera P, según mi cálculo, como la longitud FG, y por tanto infinita en el Centro, según la circunferencia se hace mínima. En cambio la luz total dentro del círculo menor PQ es a la luz total exterior como el área del cuadrilátero CAKP a la del triángulo PKB. Piénsese que el círculo menor PQ termina allí donde la densidad FG de la luz empieza a ser menor que la necesaria para impresionar al sentido. Y de aquí que un fuego de tres pies de anchura a la distancia de 191 382 pies a través de un telescopio de tres pies le pareció a Picard de casi 8” de ancho, cuando debió parecerle de 3”14’ de ancho. De aquí que las más brillantes de las fijas aparezcan con amplitudes de 5” o 6”; esto con luz bastante llena, pero con luz más débil se extienden más. Por esto Hewelcke, disminuyendo la apertura del telescopio, suprimió adecuadamente gran parte de la luz de la periferia, logró que el disco de la estrella apareciese recortado más nítidamente y resultase menor, aunque ahora también apareciese, con amplitudes de 5” o 6”. Huygens, oscureciendo un poco los cristales del ocular, suprimió en tal grado toda luz difusa que las estrellas parecían carecer de amplitud, como si fueran puntos. Por esto es por lo que Huygens, con una anchura de obstáculo tal que impidiese cualquier luz, obtuvo diámetros de los planetas mayores que los obtenidos por los demás con micrómetro: pues la luz difusa, que envuelve al planeta, se divisa más amplia al no ser oscurecida después por rayos más fuertes. Y, finalmente, por esto es por lo que los planetas en el Sol aparecen tan pequeños, atenuados por la luz extendida. Así Mercurio no superó para Hewelcke, para Gallet ni para Halley los 12” o 15”, y Venus solo pareció ocupar 1‘, 3” según Crabtrie y 1‘, 12” según Horrokcs, el cual, sin embargo, según las medidas de Hewelcke y Huygens tomadas fuera del disco solar debería ocupar como mínimo 84”. Del mismo modo el diámetro aparente de la Luna que fue medido el año 1684 en el observatorio de París pocos días antes y después del eclipse de Sol cifrándolo en 31’30”, en el eclipse no superaba 30’ o 30’5”. Así pues, los diámetros de los planetas deben disminuirse en algunos segundos cuando están fuera del disco solar y deben aumentarse también en algunos segundos cuando están dentro. Pero en cambio en las medidas efectuadas con micrómetro los errores parecen ser por lo general menores. El semidiámetro de Júpiter calculado por el diámetro de la sombra en los eclipses de los satélites, fue establecida por Flamsteed respecto a la elongación máxima del satélite exterior como de 1 a 24 903. De donde, habida cuenta que dicha elongación viene a ser de 8’13”, el diámetro de Júpiter será de 39. Por tanto el diámetro de 40” o 41” hallado con el Micrómetro, descartada la luz errática, se reduce a 39 ”. Y con una corrección similar hay que corregir el diámetro de Saturno de 21” y establecerlo en 20” o un poco menos. Pero el diámetro del Sol, al ser la luz más fuerte, ha de disminuirse, si no me equivoco, un poco más y establecerse en 32’ o en 32’6”.

17. Por qué algunos planetas son más densos y otros menos, y las fuerzas son como la cantidad de materia en cada uno

Ciertamente no deja de ser misterioso que los cuerpos celestes, siendo tan diversos de tamaño, alcancen tan gran analogía con las fuerzas. Es posible que los planetas lejanos, por falta de calor, carezcan de aquellas sustancias metálicas y de minerales pesados de que se halla abastecida la Tierra; y que los cuerpos de Venus y Mercurio, con mayor calor solar, estén más secos y compactos. Consta por el experimento del espejo ustorio que el calor aumenta con la densidad de la luz; y esta aumenta según el cuadrado de la proximidad al Sol. De aquí se sigue que el calor del Sol es en Mercurio siete veces mayor que entre nosotros en verano; pero con tanto calor el agua hierve y los otros vapores pesados del vitriolo y del Mercurio poco a poco se evaporan, como he descubierto con el termómetro: por tanto en Mercurio no subsisten elementos líquidos, a no ser los más pesados, que soportan gran calor y que dan lugar a sustancias sumamente densas. Pues que, si Dios hubiese colocado a cada cuerpo, atendiendo al conveniente calor del clima, a cada distancia del Sol; y por tanto siempre se hallarán los más densos cuanto más cerca del Sol: esto sería una buena razón para que los pesos de los planetas sean entre sí como las fuerzas. Quisiera, sin embargo, definir más exactamente los diámetros de los planetas. Esto ocurrirá, si a una gran distancia una lámpara luce a través de un agujero circular y se disminuye tanto la luz de la lámpara como el agujero hasta el punto de que la imagen vista por el telescopio aparezca semejante a un planeta, y quedará definido por estas mismas medidas. Entonces la anchura del agujero será a su propia distancia al cristal del objetivo como el auténtico diámetro del planeta a su propia distancia a nosotros. La luz de la lámpara puede disminuirse con paños o con un cristal ahumado.

18. Otra analogía entre fuerzas y cuerpos. Se prueba en los celestes

A la analogía ya descrita es afín otra entre fuerzas y cuerpos atraídos. Puesto que la acción de la fuerza centrípeta sobre los planetas decrece en razón al cuadrado de la distancia y el tiempo periódico aumenta en razón sesquiáltera; es evidente que las acciones sobre planetas iguales a iguales distancias del Sol, serán iguales y también iguales los tiempos periódicos: y que a distancias iguales de planetas desiguales las acciones en conjunto serán como los cuerpos de los planetas. Puesto que las acciones que no fuesen como los cuerpos a mover no podrían retraer por igual a dichos cuerpos de las tangentes de las órbitas, y hacer, por consiguiente, que, en tiempos iguales, se completen órbitas también iguales. Y tampoco podrían ser tan regulares los movimientos de los satélites de Júpiter, a no ser que la fuerza circumsolar se ejerciera por igual sobre Júpiter y todos los satélites, según los pesos de cada uno. La misma razón vale para Saturno y su satélite; así como para nuestras Tierra y Luna, como es evidente (por los Cor. l. 2 y 3 de la Prop. LXV). La acción de la fuerza centrípeta, por tanto, sobre los planetas es igual a distancias iguales, en razón de los cuerpos, esto es, en razón de la cantidad de materia en los cuerpos; y por tanto también sobre todas las partículas de la misma cantidad, de las que están compuestos los planetas. Pues si la acción fuese mayor sobre las partículas de una clase y menor sobre las de otra que en razón de la cantidad de materia, también sería menor o mayor la acción sobre los planetas, y no solo en razón de la cantidad de materia, sino según la clase de la misma que se hallase en ellos, en unos más, en otros menos abundante.

19. Se prueba en los cuerpos terrestres

En verdad he estudiado muy detalladamente la analogía en los cuerpos sumamente diversos que hay en la Tierra. La acción de la fuerza circumterrestre, proporcional a los cuerpos que se han de mover, moverá a los susodichos cuerpos en tiempos iguales y con velocidad igual (por la Ley 2 del Movimiento) y hará que tanto los cuerpos todos que caen en tiempos iguales recorran espacios iguales, como que todos los cuerpos que estén suspendidos por hilos iguales oscilen en tiempos iguales. Con una acción mayor los tiempos serán menores y con una menor, mayores. Que la caída de todos los cuerpos (descontada al menos la insignificante resistencia del aire) se realiza en tiempos iguales ya lo han observado otros; y es posible observar con toda exactitud la igualdad de los tiempos en los péndulos. He hecho pruebas con oro, plata, plomo, vidrio, arena, sal común, madera, agua, trigo. Comparaba dos cajas de igual forma y tamaño; llenaba una de madera y pegaba en el centro de oscilación de la otra un peso de oro igual (con la mayor exactitud que pude) al otro. Las cajas colgadas de hilos iguales de once pies constituían péndulos totalmente iguales en cuanto a pesos, figuras y resistencia del aire; y yuxtapuestas iban y venían a la vez durante largo tiempo en oscilaciones iguales. Por tanto la cantidad de materia en el oro era a la cantidad de materia en la madera como la acción de la fuerza motriz sobre todo el oro a la acción de la misma sobre toda la madera; esto es como peso a peso; y lo mismo en los demás. En cuerpos del mismo peso la diferencia de materia, incluso siendo menor que la milésima parte del total de materia, podría determinarse claramente con estos experimentos.

20. Convergencia de Analogías

Puesto que la acción de la fuerza centrípeta sobre el cuerpo atraído, a distancias iguales, es proporcional a la cantidad de materia de este último, es razonable también que sea proporcional a la cantidad de materia del cuerpo que atrae. Así pues la acción es mutua, y hace que los cuerpos se atraigan mutuamente con acciones mutuas (por la Ley 3 del Movimiento) y por tanto debe ser conforme a cada uno de los dos cuerpos. Puede considerarse a un cuerpo como atrayente y al otro como atraído, pero esta distinción es más matemática que natural. En realidad la atracción es de cada cuerpo sobre cada cuerpo y por tanto del mismo género en todos.

21. Y coincidencia

Y por esto es por lo que la fuerza atractiva se halla en cada uno. El Sol atrae a Júpiter y al resto de los planetas. Júpiter atrae a los satélites, y por la misma razón los satélites actúan mutuamente entre sí y sobre Júpiter, y todos los planetas entre ellos. Y aunque las acciones mutuas de dos planetas podrían distinguirse entre si y ser consideradas como dos acciones mediante las cuales cada uno atrae al otro, sin embargo, en tanto que son intermedias, no son dos, sino una operación simple entre dos términos. Por la contracción de un solo cordón interpuesto entre ellos pueden dos cuerpos ser atraídos entre sí. La causa de la acción es doble, claramente la disposición de uno y otro cuerpo; pero en tanto que es entre dos cuerpos, es simple y única. No es una la operación por la que el Sol atrae por ejemplo a Júpiter y otra operación aquella por la que Júpiter atrae al Sol, sino una operación por la que el Sol y Júpiter intentan acercarse entre sí, por la acción por la que el Sol atrae a Júpiter intentan Júpiter y el Sol acercarse entre sí (por la Ley 3 del movimiento) y por la acción por la que Júpiter atrae al Sol, intentan también Júpiter y el Sol acercarse mutuamente; el Sol, pues, no es atraído hacia Júpiter por una acción doble y tampoco lo es Júpiter hacia el Sol, sino que hay una sola acción intermedia por la que ambos tienden uno hacia otro. El hierro atrae al imán igual que el imán al hierro, pues todo hierro en contacto con un imán atrae también a otro hierro. Pero la acción entre el imán y el hierro es simple y como tal es vista por los filósofos; la operación del hierro sobre el imán es la misma operación del imán entre el mismo y el hierro, por la que ambos tienden a acercarse entre sí. Esto se ve por el hecho de que, al suprimir el imán, cesa de inmediato toda la fuerza del hierro. De modo similar hay que concebir entre dos planetas la operación simple que surge de la naturaleza cooperante de ambos, y también de este modo se comportará con respecto a cada uno de ellos, hasta el punto de que siendo proporcional a la materia en uno de ellos, será proporcional a la materia en el otro.

22. Las fuerzas de los cuerpos pequeños son insensibles

Quizá alguien diga que el que todos los cuerpos deban atraerse mutuamente según esta Ley es contra la experiencia en los cuerpos terrestres. Pero respondo que la experiencia en los cuerpos terrestres prácticamente no existe. Las atracciones de esferas homogéneas en las inmediaciones de su superficie son (por la Proposición LXXII) como los diámetros; de donde una esfera, homogénea a la Tierra y de un pie de diámetro atrae a un corpúsculo en las inmediaciones de su superficie casi 20 000 000 de veces menos que la Tierra en las suyas; y tan minúscula fuerza no produce efecto observable alguno. Igualmente dos de tales globos distantes entre sí solo la cuarta parte de un codo no se juntarían, en el espacio libre, y en razón de la fuerza de atracción mutua en menos del intervalo de un mes. El encuentro de globos menores sería más lento en razón del diámetro. Y ni siquiera bastarían todos los montes para hacer sensibles los efectos: al pie de un monte semiesférico de tres millas de alto y seis de ancho, un péndulo, atraído por la fuerza del monte, no se desviará de la perpendicular en dos minutos. Semejantes fuerzas solo es posible intuirlas en las ingentes masas de los planetas; salvo que discutamos sobre partes más pequeñas de este modo.

23. Las fuerzas por las que tienden los cuerpos terrestres son proporcionales a la cantidad de materia

Sea EFGI el globo terrestre cortado por un plano cualquier EG en dos partes EFG, EIG. La parte EFG, al apoyarse sobre la parte EIG la oprime con todo su peso. Pero la parte EIG no podría sostener esta presión y permanecer inmóvil, a no ser con un empuje igual y en sentido contrario. Las partes, pues, se empujan mutuamente con sus pesos de igual modo, esto es, se atraen entre sí de igual modo, como exige la tercera Ley; y además separadas una de otra y sueltas caerían una hacia otra mutuamente con velocidades que fuesen recíprocamente como los cuerpos. Todo lo cual es posible ver y experimentar con el Imán. Sea ahora EFG un cuerpo pequeño en la superficie de la Tierra; y puesto que las atracciones de esta partícula y de todo el resto EIG de la Tierra entre sí son mutuamente iguales, pues la atracción de la partícula hacia la Tierra (esto es su peso) es como la materia de la partícula, según se ha probado por el experimento del péndulo, también será la atracción de la Tierra hacia la partícula como la materia de la partícula; y por canto las fuerzas atractivas de todos los cuerpos terrestres serán como la cantidad de materia en cada uno.

24. Se prueba que dichas fuerzas tienden a los cuerpos celestes

Por tanto las fuerzas, que son como la materia en todos los cuerpos terrestres sea cual sea la forma que tengan y, por tanto, no cambian con el cambio de forma, deben estar presentes en todos los cuerpos tanto celestes como terrestres, y ser en todos proporcionales a la materia; y ello precisamente porque todas ellas no se distinguen por el tipo de materia sino por solo las formas y las modificaciones. Esto se prueba también en los cuerpos celestes del modo siguiente. Se ha probado que la acción de la fuerza circumsolar sobre todos los planetas, colocados a iguales distancias, es como la materia en dichos planetas; esto también consta de modo semejante de la acción circumjovial sobre los satélites de Júpiter; y también es la misma la razón de la atracción de todos los planetas sobre cada uno de ellos. De donde se sigue (por la Propos. LXIX) que sus fuerzas atractivas son como la materia en cada uno de ellos.

25. Las fuerzas decrecen desde la superficie de los planetas hacia afuera en rezón al cuadrado de la distancie al centro, y hacia dentro en rezón de la distancia

Así pues, como las partes de la tierra se atraen mutuamente, del mismo modo lo hacen las partes de los planetas. Si Júpiter y sus satélites se reunieran y formasen un solo globo, sin duda cada uno de ellos pasaría a atraerse como antes, y viceversa, si el cuerpo de Júpiter se rompiese en varios globos, hay que creer que estos no se atraerían entre sí menos de lo que atraen los satélites. A estas atracciones se debe el hecho de que los cuerpos de la Tierra y de todos los planetas adopte una forma esférica, y de que sus partes estén cohesionadas y no se dispersen por el aire. Ya se ha demostrado que todas estas fuerzas tienen su origen en la naturaleza universal de la materia, y por tanto la fuerza de todo el globo se compone de las fuerzas de las partículas. Y de aquí se sigue (por el Cor. 3 de la Prop. LXXIV) que la fuerza de cualquier partícula decrece en razón del cuadrado de la distancia de esa partícula; y (por las Props. LXXIII y LXXV) que la fuerza del globo entero decrece desde su superficie hacia afuera según el cuadrado de la distancia al centro y hacia adentro en razón simple de la distancia al mismo centro, siempre que el globo esté constituido de materia uniforme; y aunque los globos desde el centro a la superficie no sean uniformes, seguirá valiendo hacia afuera el decremento en razón del cuadrado de la distancia (por la Prop. LXXVI), siempre que la desigualdad sea parigual en el decurso desde el centro a la superficie; y dos globos de este tipo (por la misma proposición) se atraerán mutuamente con una fuerza decreciente en razón del cuadrado de las distancias entre los centros.

26. Magnitudes de las fuerzas y de los movimientos nacidos de ellas en cada caso

Por lo tanto la fuerza absoluta de cualquier globo es como la cantidad de materia que hay en él. La fuerza motriz, en cambio, por la que un globo cualquiera es atraído hacia otro, y a la que el vulgo en los cuerpos terrestres designa con el nombre de peso, es como el total de las cantidades de materia contenidas en ambos globos dividido por el cuadrado de la distancia entre los centros (por el Cor. 4 de la Prop. LXXVI) y la cantidad de movimiento es proporcional a esta fuerza, cantidad con la que cada globo se moverá hacia el otro en un tiempo dado: la fuerza aceleratriz, en cambio, con la que cada uno de los globos en razón de su propia cantidad de materia, es atraído hacia el otro, es como la cantidad de materia del otro dividida por el cuadrado de la distancia entre centros (por el Cor. 2 de la Prop. LXXVI), y a esta fuerza es proporcional la velocidad con la que el globo atraído se mueve, en un tiempo dado, hacia el otro. Una vez comprendido esto correctamente, será muy fácil determinar los movimientos de los cuerpos celestes entre sí.

27. Todos los planetas giran en tomo al Sol

Hemos visto que, reunidas las fuerzas de los planetas, la fuerza circumsolar es mil o más veces superior a ellas. Bajo la acción de tamaña fuerza es necesario que todos los cuerpos dentro del espacio interplanetario y mucho más allá caigan rectamente hacia el Sol; a no ser que se muevan de otro modo. Ni siquiera la Tierra ha de ser excluida del número de tales cuerpos. La Luna con certeza es del género de los planetas, y sometida a las mismas atracciones que el resto de los planetas: pero retenida en su órbita por la fuerza circumterrestre. Ya hemos probado más arriba que la Tierra y la Luna son atraídas por igual hacia el Sol; y además ya hemos probado anteriormente que todos los cuerpos están sometidos a iguales leyes de atracción. En cuánto tiempo, en cambio, cada cuerpo, privado de movimiento circular, descendería y llegaría a caer hasta el Sol, se deduce (por la Prop. XXXVI) de su distancia al Sol: A saber, en la mitad del tiempo periódico en que el cuerpo a una distancia dos veces menor puede girar.[5] O también en el tiempo que sea al tiempo periódico del planeta como 1 a . Como que Venus cayendo llegaría al Sol en el espacio de cuarenta días; Júpiter en el espacio de dos años y un mes; la Tierra y la Luna en el espacio de sesenta y seis días y diecinueve horas.[6] Como tal cosa no acontece es preciso que se muevan de otro modo; pero no basta cualquier movimiento; para impedir la caída es necesaria una velocidad bastante grande. Por ello sirve el argumento también para los planetas que se desaceleran. Salvo que la fuerza circumsolar decrezca en razón del cuadrado de la desaceleración, su exceso haría que los cuerpos cayesen hacia el Sol: por ejemplo, si el movimiento, caeteris paribus, se hiciese el doble de lento, el planeta sería retenido en su órbita por la cuarta parte de la fuerza circumsolar anterior y con el exceso de las otras tres cuartas partes caerá hacia el Sol. Por tanto los planetas, Saturno, Júpiter, Marte, Venus y Mercurio no se retrasan realmente en los perigeos ni se hacen realmente estacionarios o levemente retrógrados. Todo esto son solo apariencias; y los movimientos absolutos con los que los planetas perseveran en sus órbitas son siempre directos y casi constantes. Hemos probado que tales movimientos se efectúan en torno al Sol y por tanto el Sol, en tanto que centro de tales movimientos absolutos, está en reposo: así pues, el reposo de la Tierra debe ser rechazado absolutamente para que los planetas en los perigeos no se retarden realmente, ni se hagan estacionarios de verdad ni lentamente retrógrados y, al faltarles el movimiento vengan así a caer en el Sol. Por lo demás, puesto que los planetas Venus, Marte, Júpiter, etc., con los radios trazados al Sol describen órbitas regulares y áreas proporcionales a los tiempos según las observaciones como ya se ha mostrado; se sigue en consecuencia que (por la Prop. III y por el Cor. 3 de la Prop. LXV) el Sol no es influido por ninguna fuerza notable, salvo aquella que ejercen los planetas todos por igual según la cantidad de materia de cada cuerpo y según líneas paralelas y por tanto todo el sistema se desplaza en línea recta. Prescindamos de este desplazamiento de todo el sistema y el Sol reposa más o menos en el centro del mismo. Si el Sol girase en torno a la Tierra y llevase en torno al resto de los planetas, la Tierra habría de atraer al Sol con una gran fuerza; los planetas circunvolares en cambio con ninguna fuerza que tuviese efectos sensibles (absolutamente contra el Corolario 3 de la Prop. LXV). Añádase además que si la Tierra, por la gravedad de las partes, ha sido ubicada por casi todos hasta aquí en la región inferior del mundo, ahora el Sol con mucha más razón por su fuerza centrípeta mil y más veces mayor que la gravedad terrestre deberá situarse en el lugar más bajo y constituir el centro del sistema. De este modo se comprende más completa y exactamente la verdadera constitución del sistema.

28. El centro común de gravedad de todos los planetas está en reposo y el Sol se mueve muy lentamente. Se define el movimiento del Sol

Puesto que las fijas están entre sí en reposo, imaginemos al Sol, la Tierra y los planetas como un sistema de cuerpos moviéndose de cualquier modo entre sí y el centro de gravedad común de todos ellos (por el Cor. cuarto de las Leyes) o está en reposo o se mueve uniformemente en línea recta. En este segundo caso también el sistema entero se moverá en línea recta. Dura es esta hipótesis: descartada ella, permanecerá en reposo el centro común de gravedad. De tal centro el Sol nunca se aparta mucho. El centro común de gravedad del Sol y de Júpiter cae en la superficie del Sol.[7] Si todos los planetas se sitúan a la vez que Júpiter hacia el mismo lado del Sol, el centro común del Sol y todos los planetas apenas se apartará del Centro del Sol en más del doble que antes.[8] Por tanto el Sol, influido aleatoriamente por las diferentes situaciones de los planetas, y deambulando siempre lentamente con un movimiento libratorio, jamás llega a desviarse en la cuantía de su diámetro del centro en reposo del sistema. El centro común de gravedad se obtiene, pues, a partir de los pesos hallados más arriba del Sol y de los planetas y de las situaciones relativas entre todos ellos: y, una vez determinado aquel, el lugar del Sol en el momento propuesto.

29. Los planetas giran en elipses cuyos focos están en el Sol; y con radios trazados al Sol describen áreas proporcionales a los tiempos

Todos los planetas giran en torno al Sol, con su libración susodicha, en órbitas elípticas, y con radios trazados al Sol describen áreas muy aproximadamente proporcionales a los tiempos, como se ha expuesto (en la Prop. LXV). Si el Sol reposase y los planetas restantes no actuasen entre sí, las órbitas serían elípticas y las áreas exactamente proporcionales a los tiempos (por la Prop. XI y el Cor. I de la Prop. XIII). Las acciones mutuas de los planetas, comparadas con las acciones del Sol entre los planetas carecen de importancia, y por tanto no inducen a ningún error apreciable: y vienen a ser esos errores más pequeños en las revoluciones en torno al Sol inestabilizado del modo descrito, que en las revoluciones en torno al Sol en reposo (por la Prop. LXVI y el Cor. de la Prop. LXVIII) sobre todo si el foco de cualquier órbita se ubica en el centro común de gravedad de todos los planetas interiores: o sea el foco de la órbita de Mercurio en el centro del Sol, el foco de la órbita de Venus en el centro común de gravedad de Mercurio y el Sol, el foco de la órbita de la Tierra en el centro común de gravedad de Venus, Mercurio y el Sol; y así sucesivamente. De este modo los focos de todas las órbitas de todos los planetas, con excepción de Saturno, no distarán sensiblemente del centro del Sol; ni siquiera el foco de la órbita de Saturno se apartará sensiblemente del centro común de gravedad de Júpiter y el Sol. Por tanto no se equivocan mucho los astrónomos al establecer el foco común de todas las órbitas en el centro del Sol. En el mismo Saturno el error que se sigue de hacerlo así no es mayor de 1’45”. Si esta órbita, situando el foco en el centro común de gravedad de Júpiter y el Sol, se ajustase mejor a los fenómenos, se confirmaría por ello todo esto que hemos dicho.

30. De las dimensiones de las órbitas y del movimiento de Afelios y Nodos

Si el Sol estuviese en reposo y los planetas nada se influyesen unos a otros, también estarían en reposo sus Afelios y Nodos (por las Prop. I, XI, y el Cor. de la Prop. XIII) y los ejes mayores de las órbitas elípticas serían como los lados (raíces) cúbicos de los cuadrados de los tiempos periódicos (por la Prop. XV) y por tanto vendrían dados a partir de los tiempos periódicos también dados. Habrán de medirse estos tiempos, no a partir de los puntos móviles de los equinoccios, sino a partir de la primera estrella de Aries. Pero el semieje aumenta un tanto por el movimiento del Sol, casi la tercera parte de la distancia desde el centro del Sol al centro común de gravedad del Sol y el planeta (por la Prop. LX) y por las acciones de los planetas exteriores sobre los interiores aumenta algo el tiempo periódico de los interiores, aunque apenas perceptiblemente, y como consecuencia los Afelios se mueven muy lentamente (por los Cor. 6 y 7 de la Prop. LXVI) y lo mismo por las acciones de los cometas, si es que alguno llegase más allá de Saturno, aumentarán los tiempos periódicos de todos los planetas, y sobre todo los de los exteriores: y los Afelios de todos se moverán en consecuencia. Al progreso de los Afelios corresponde el retroceso de los Nodos (por los Cor. 11 y 13 de la Prop. LXVI) y su retroceso, si el plano de la Eclíptica estuviese en reposo, será al progreso de los Afelios (por el Cor. 16 de la Prop. LXVI) en cada órbita, como el retroceso de los Nodos de la Luna al progreso de su Afelio muy aproximadamente; esto es como 10 a 21 aproximadamente. Parece que las observaciones astronómicas confirman que los Afelios progresan muy lentamente y los Nodos retroceden de igual modo, respecto a las fijas. Y por ello, es verosímil que los Cometas discurran por regiones ultra planetarias. Los tales cometas girando en órbitas muy excéntricas, recorren a gran velocidad sus Perihelios y con un movimiento muy lento en sus Afelios, consumen casi todo el tiempo en regiones supraplanetarias, como se verá después más ampliamente.

31. De los principios aducidos se derivan todos los movimientos de la Luna observados por los astrónomos hasta ahora

Ya se sabe (por la proposición LXV) que los planetas que giran de este modo pueden arrastrar en torno a sí a otros, o Satélites, o Lunas. Pero por la acción del Sol sucede que nuestra Luna se mueve más rápidamente, y que con su radio trazado a la Tierra describe un área mayor en relación con el tiempo, y tenga una órbita menos curva, y que por tanto se acerque más a la Tierra en las Sicigias que en las Cuadraturas, salvo en lo que impide el movimiento de excentricidad, pues la excentricidad es máxima cuando el Apogeo de la Luna ocurre en las Sicigias, y mínima cuando ocurre en las Cuadraturas; y por tanto la Luna en el Perigeo es más rápida y más cercana a nosotros; en el Apogeo en cambio es más lenta y más lejana en las Sicigias que en las Cuadraturas. Además el Apogeo progresa y se retrasan los Nodos, pero con movimiento desigual; y el Apogeo ciertamente progresa más velozmente en sus Sicigias y retrocede más lentamente en las Cuadraturas y el exceso del progreso sobre el retroceso, se toma anualmente en consideración. Los Nodos, en cambio, reposan durante sus Sicigias y retroceden muy rápidamente durante las Cuadraturas. Y además es mayor la anchura máxima de la Luna en sus Cuadraturas que en las Sicigias; y el movimiento medio más lento en el Perihelio de la Tierra que en su Afelio. Muchas desigualdades en el movimiento de la Luna aún no son observadas por los astrónomos. Sin embargo, todas ellas se siguen de nuestros principios (por los Cor. 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13 de la Prop. LXVI) eaey se sabe que efectivamente ocurren en los cielos. Se puede ver esto en la hipótesis de Horrokcs por demás ingeniosa y, si no me equivoco, la más adecuada de todas, que Flamsteed adaptó a los Cielos. Sin embargo hay que corregir las hipótesis astronómicas en los movimientos de los Nodos. Estas admiten una ecuación máxima o prostaféresis en sus octantes, siendo así que la desigualdad es muy notable cuando la Luna transita por los Nodos y en consecuencia por los octantes. Así que Tycho, y otros después de él, rechazaron esta desigualdad en los octantes de la Luna, y la hicieron mensual. Pero las razones expuestas por nosotros enseñan que debe ser referida a los octantes de los Nodos y hacerse anual.

32. Y que también otros varios movimientos observados de los Nodos son desiguales

Además de las desigualdades registradas por los astrónomos, hay otras cuantas, que perturban los movimientos de la Luna hasta el punto de que hasta ahora no han podido ser reducidas a regularidad alguna cierta por Ley ninguna. Pues las velocidades, o movimientos horarios, del Apogeo y Nodos de la Luna, y sus ecuaciones, así como la diferencia entre la excentricidad máxima en las Sicigias y la mínima en las Cuadraturas, y la desigualdad llamada Variación, aumentan y disminuyen anualmente (por el Cor. 14 de la Prop. LXVIa) en razón del cubo del diámetro aparente del Sol. La Variación además está en razón del cuadrado, muy aproximadamente, del tiempo entre Cuadraturas (por los Cor. 1 y 2 del Lema X y el Cor. 16 de la Prop. LXVI). Y todas estas desigualdades son en la parte de la órbita más cercana al Sol un poco mayores que en la parte opuesta, pero la diferencia es apenas o, ni apenas, sensible.

33. Y la distancia de la Luna a la Tierra en un momento dado

Por medio de un cálculo, que no describo por mor de la brevedad, hallo también que el área que la Luna describe con un radio a la Tierra en cada parte igual y pequeña de tiempo es muy aproximadamente como la suma de los números 237 y el seno verso del doble de la distancia de la Luna a la Cuadratura próxima, en un círculo cuyo radio es la unidad; y por tanto que el cuadrado de la distancia de la Luna a la Tierra es como la suma susodicha dividida por el movimiento horario de la Luna.[9] Así es esto, cuando la Variación en los octantes es de una magnitud media; pero, cuando es mayor o menor, el seno verso mencionado debe aumentarse o disminuirse en la misma proporción. Prueben los astrónomos cuán aproximadamente las distancias así halladas se acuerdan con los diámetros aparentes de la Luna.

34. Del movimientos de la Luna se derivan los de los Satélites de Júpiter y Saturno

De los movimientos de nuestra Luna es posible derivar los movimientos de las Lunas o Satélites de Júpiter y Saturno. Pues el movimiento medio de los Nodos del satélite exterior de Júpiter es al movimiento medio de los Nodos de nuestra Luna en razón compuesta de la razón cuadrada del tiempo periódico de Júpiter en torno al Sol y la razón simple del tiempo periódico de la Luna en torno a la Tierra (por el Cor. 16 de la Prop. LXVI) y por tanto este Nodo, en cien años, se desplaza 8º 24’ hacia atrás. Los movimientos medios de los Nodos de los satélites interiores son al movimiento de este, como sus tiempos periódicos al tiempo periódico del mismo (por el mismo Corolario) y de aquí que estén dados. El movimiento pues del Apogeo de un satélite cualquiera hacia adelante es al movimiento de sus Nodos hacia atrás como el movimiento del Apogeo de nuestra Luna al movimiento de sus Nodos (por el mismo corolario) y de aquí que esté dado. Las ecuaciones máximas de los Nodos y del Apogeo de un satélite cualquiera son a las ecuaciones máximas de los Nodos y del Apogeo de la Luna respectivamente, como los movimientos de los Nodos y del Apogeo de los satélites, en el tiempo de una revolución de las ecuaciones anteriores, a los movimientos de los Nodos y del Apogeo de la Luna en el tiempo de una revolución de las ecuaciones posteriores. La Variación del satélite, visto desde Júpiter, es a la Variación de la Luna, como son los movimientos todos unos a otros entre sí de los Nodos en los tiempos periódicos del Satélite y de la Luna (por el mismo Corolario) y por tanto en el satélite exterior no es superior a 5’12”. La pequeñez de estas desigualdades y la lentitud de los movimientos hacen que los movimientos de los satélites aparezcan tan regules, y que los astrónomos más recientes, o bien nieguen todo movimiento nodal, o bien lo consideren muy lentamente regresivo.

35. Los planetas giran sobre sus ejes con movimiento uniforme respecto a las fijas. Este movimiento es muy adecuado para la medida del tiempo

Mientras los planetas giran de este modo en torno a centros lejanos, rotan cada uno en torno a su propio eje. El Sol en 26 días; Júpiter en 9 horas y 56 minutos; Marte en 24 horas; Venus en 23 horas; y esto en planos no muy inclinados con respecto al plano de la Eclíptica, y según el orden de los signos; tal y como los astrónomos lo determinan a partir de las manchas que hay en sus cuerpos y que van pasando alternativamente ante la observación. Semejante es la revolución de nuestra Tierra completada en 24 horas. Consta que estos movimientos ni se aceleran ni se retardan por las acciones de las fuerzas centrípetas (por el Cor. 22 de la Prop. LXVI). Son además uniformes por encima de todos los demás y por tanto sumamente adecuados para medir el tiempo. Pero las revoluciones deben ser adecuadas no por el retorno al Sol, sino por el retorno a una estrella fija. Puesto que la situación de los planetas con respecto al Sol varía de modo no uniforme, sus revoluciones de Sol a Sol se hacen también no uniformes.

36. De modo semejante la Luna gira sobre su eje con movimiento diurno, y de aquí procede su movimiento libratorio

Del mismo modo la Luna gira sobre su propio eje con movimiento sumamente uniforme respecto a las fijas. Gira, efectivamente, en el tiempo de 27 días, 7 horas y 43 minutos, esto es en un mes sidéreo, de tal modo que este movimiento diurno es igual al movimiento medio de la Luna en su órbita. Por eso la misma cara de la Luna está dirigida siempre hacia el centro en torno al cual se efectúa este movimiento medio; esto es, hacia el foco externo de la órbita lunar muy aproximadamente. De aquí surge la desviación de la cara de la Luna respecto a la Tierra, ya hacia oriente, ya a occidente según el lugar del foco al que se orienta; tal desvío es igual a la prostaféresis de la órbita lunar, o diferencia entre el movimiento medio y el real. Esta es la libración de la Luna en sentido longitudinal, y en sentido latitudinal la libración surge de la inclinación del eje lunar respecto al plano de la órbita en que gira la Luna en torno a la Tierra. Dicho eje sin embargo mantiene su posición respecto a las fijas muy aproximadamente, y por ello los polos pasan ante nuestros ojos alternativamente. Es posible ilustrar esto a la luz del movimiento de la Tierra, cuyos polos, debido a la inclinación de su eje sobre el plano de la eclíptica son iluminados por el Sol alternativamente. Determinar la posición del eje respecto a las fijas y la variación de esta posición es problema digno de un Astrónomo.

37. De la precesión de los equinoccios y del movimiento libratorio del eje de la Tierra y de los planetas

Debido a las revoluciones diarias de los planetas la materia tiende a separarse de los ejes de dicho movimiento; y por ello las partes líquidas se elevan más en el ecuador que en los polos e inundarán a las partes sólidas salvo que se eleven por igual. Por ello los planetas son algo más anchos por el ecuador que por los polos, y por ello sus puntos equinocciales retroceden; y los ejes oscilan dos veces cada revolución con un movimiento de vaivén y dos veces vuelven a la primitiva inclinación; como se ha expuesto en el Corolario 18 de la Prop. LXVI. Y por ello Júpiter contemplado a través de telescopios muy largos aparece no completamente redondo, sino que su diámetro paralelo a la Eclíptica es algo más grande que el que va de Norte a Sur.

38. El mar debe subir y bajar dos veces cada día, y la pleamar ocurre en la hora tercia desde el paso de los astros por al meridiano del lugar

Así también cada día, tanto lunar como solar, nuestro mar por el movimiento diario de la Tierra y por las atracciones del Sol y de la Luna debe crecer y decrecer dos veces (por los Cor. 19 y 20 de la Prop. LXVI) y la altura máxima del agua debe preceder a la hora sexta de cada día y seguir a la duodécima precedente. Por la lentitud del movimiento diario, la marea se retrae hasta la hora duodécima y por la fuerza del movimiento de reciprocación se prolonga hasta una hora lo más cerca posible de la Sexta. Entre tanto, mientras determinemos el tiempo más exactamente por los fenómenos, ¿por qué no fijar la pleamar, reteniendo el punto medio del tiempo, en la hora tercia? De este modo el agua sube durante todo el tiempo en que la fuerza de los astros que se aplica a ella es mayor, y desciende durante todo el tiempo en que es menor, puesto que dicha fuerza es mayor desde la hora nona a la hora tercia y menor desde la hora tercia a la nona. Cuento las horas desde el paso de cada astro por el meridiano del lugar, tanto sobre como bajo el horizonte; y por horas del día lunar entiendo las vigesimocuartas partes del tiempo en el que la Luna con su movimiento diario aparente, retorna al meridiano del lugar.

39. Las mareas máximas ocurren en las Sicigias de los astros y la Tierra, las mínimas en las Cuadraturas; y esto a la hora tercia del paso de la Luna por el meridiano del lugar; pero fuera de las Sicigias y de las Cuadraturas se desvía un tanto de dicha hora tercie hacia la hora tercia del peso del Sol

Los movimientos que producen los pasos de los dos astros, no se aprecian como movimientos distintos, sino que constituyen una suerte de movimiento mixto. La conjunción u oposición de los astros juntan sus efectos y componen flujos y reflujos máximos. En las Cuadraturas el Sol abomba el agua mientras la Luna la aplana; y la deprime cuando la Luna la abomba; y de la diferencia de ambos efectos surge la marea más pequeña. Y puesto que, testigo la experiencia, es mayor el efecto de la Luna que el del Sol, ocurrirá la mayor altura del agua en la hora tercia lunar. Fuera de las Sicigias y Cuadraturas, la marea máxima que se deba a la sola fuerza lunar deberá siempre coincidir con la hora tercia lunar, y la que se deba a la sola fuerza solar deberá coincidir con la hora tercia solar; con las fuerzas compuestas coincidirá con un momento intermedio que estará más cerca de la tercia lunar; y por ello, en el tránsito de la Luna de las Sicigias a las Cuadraturas, cuando la hora tercia solar precede a la lunar, la máxima altura del agua precede también a la tercia lunar, y esto con intervalo máximo poco posterior a los octantes de la Luna; y con intervalos similares la marea máxima seguirá a la hora tercia lunar en el paso de la Luna de las Cuadraturas a las Sicigias.

40. Las mareas son mayores cuando los astros están en los Perigeos

Pero los efectos de los astros dependen de su distancia a la Tierra. En las distancias, pues, menores los efectos son mayores y en las mayores menores, y esto en razón del cubo de los diámetros aparentes. Por tanto el Sol en invierno, al estar en el perigeo, produce mayores efectos, y hace que las mareas en las Sicigias sean mayores y en las Cuadraturas menores (coeteris paribus) que en verano; y la Luna en el Perigeo cada mes causa mayores mareas que antes o después del día quince cuando discurre por el Apogeo. De donde ocurre que de ningún modo se sigan dos marcas máximas seguidas en Sicigias continuas.

41. Las mareas son mayores hacia los Equinoccios

Dependen también los efectos de uno y otro astro de su inclinación o distancia del Ecuador. Pues si un astro se situase en un polo, atraería hacia allí constantemente a cada parte de agua sin aumento ni disminución de la acción, y por tanto no habría ningún movimiento de reflujo. Por tanto los astros apartándose del Ecuador hacia el polo, producen sus efectos gradualmente y por tanto serán menores las mareas en las Sicigias de los Solsticios que en las de los Equinoccios. En cambio en las Cuadraturas Solsticiales las mareas serán mayores que en las Equinocciales; precisamente por el hecho de que los efectos de la Luna una vez situada en el Ecuador superan en el mayor grado a los efectos del Sol. Ocurren por tanto las mareas máximas en las Sicigias y las mínimas en las Cuadraturas de los astros, hacia los Equinoccios de ambos y la marea máxima en las Sicigias está siempre acompañada de la mínima en las Cuadraturas, como se ha encontrado por la experiencia. Ocurre, en cambio, por la menor distancia de la Tierra al Sol en invierno que en verano que las mareas máximas y mínimas preceden más frecuentemente que siguen al equinoccio de primavera; y también más frecuentemente siguen que preceden al de otoño.

42. Las mareas extraecuatoriles son alternativamente mayores y menores.

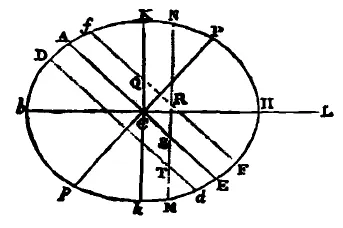
Asimismo dependen los efectos de los astros de la latitud de cada sitio. Sea ApEP la Tierra cubierta totalmente de aguas profundas, C su centro, Pp los polos, AE el Ecuador, Ff el paralelo del lugar; Dd el paralelo correspondiente al otro lado del Ecuador; L el lugar que ocupaba la Luna tres horas antes, H el lugar de la Tierra influido perpendicularmente; h el lugar opuesto al anterior; Kk los lugares distantes 90 grados de los dos anteriores; CH, ch las alturas máximas del mar medidas desde el centro de la Tierra; y CK, ck las mínimas. Si con los ejes Hh, Kk se describe una elipse; y después por revolución de esta elipse en torno al eje mayor Hh se describe el esferoide HPK hpk, esta figura representará al mar muy aproximadamente serán entonces CF, Cf, CD, Cd las alturas del mar en los puntos F, f, D, d, pero además si en la susodicha revolución de la elipse un punto cualquiera N describe un círculo MN que corta a los paralelos Ff, Dd en cualquier lugar, R, T, y al Ecuador AE en S, será CN la altura del mar en todos los lugares R, S, T, situados en este círculo. De aquí que en la revolución diaria de cualquier lugar F, el flujo será máximo en F en la hora tercia después del paso de la Luna por el meridiano supra horizonte; posteriormente el reflujo será máximo en Q en la hora tercia después del ocaso de la Luna; por ello el flujo máximo en f será en la hora tercia después de la llegada de la Luna la meridiano infra horizonte y por último el reflujo máximo en Q en la hora tercia después del Orto Lunar; y el flujo siguiente en f será menor que el flujo anterior en F. Se divide pues el mar entero en dos flujos enormes y hemisféricos: uno en el hemisferio KHkC que está orientado al Norte y el otro en el hemisferio opuesto KhkC: a los cuales podemos llamar por tanto flujo boreal y flujo austral. Estos flujos, siempre mutuamente opuestos, llegan alternativamente a los meridianos de cada lugar, con el intervalo de doce horas lunares. Y puesto que las regiones boreales participan en mayor medida del flujo boreal y las australes del austral de aquí se sigue que las mareas sean alternativamente mayores y menores en cada lugar a uno y otro lado del Ecuador. La marea mayor, pues, cuando la Luna declina hacia el vértice del lugar, coincide aproximadamente con la hora tercia después del paso de la Luna por el meridiano Supra horizonte del lugar y, al ir cambiando la declinación de la Luna, se invierte hacia la menor. La máxima diferencia de flujos cae en la época de los solsticios, sobre todo si el Nodo ascendente de la Luna pasa por el principio de Aries. Así las mareas de la mañana en invierno superan a las de la tarde, y las de la tarde en verano a las de la mañana, en Plymouth casi en un pie de altura y en Bristol en quince pulgadas de altura según las observaciones de Colepress y Sturmy.

43. Por le conservación del movimiento impreso disminuye la diferencia de las mareas y puede ocurrir también que la marea máxima mensual sea la tercera después de las Sicigias

Pero los movimientos del mar descritos hasta aquí varían un tanto por la fuerza de reciprocación de las aguas por la que la marea del mar, incluso cesando la influencia de los astros, puede permanecer durante algún tiempo. Esta conservación del movimiento impreso disminuye la diferencia de las mareas alternas; y hace a las mareas inmediatas o las Sicigias mayores, y a las inmediatas a las Cuadraturas menores. Lo que hace que las mareas alternas en Plymouth y Bristol no difieran entre sí en mucho más de un pie o quince pulgadas de altura y que las mayores mareas en dichos puertos no sean las primeras, sino las terceras después de las Sicigias.

44. El movimiento del mar se retarda por obstrucción en las cuencas marinas

También puede ocurrir que la marea mayor sea la cuarta o la quinta después de las Sicigias o que llegue más tarde, por el hecho de que los movimientos del mar se retrasen al pasar por lugares de poca profundidad camino de las costas. Así ocurre que la marea llega a la costa occidental de Irlanda a la tercera hora lunar, y después de una o dos horas a los puertos sureños de dicha isla; lo mismo que a las Casitérides, llamadas comúnmente Sorlings; después sucesivamente a Falmouth, Plymouth, Portland, la isla de Wight, Winchester, Dover, la boca del Támesis y el Puente de Londres tardando doce horas en este recorrido. Y hasta en el Océano mismo la propagación de la marea es impedida por cuencas no suficientemente profundas. Efectivamente llega la marca a las Islas Canarias y a las costas occidentales del Mar Atlántico de Irlanda, Francia, España y África toda, hasta el cabo de Buena Esperanza, en la hora tercia lunar, salvo en algunos pocos lugares poco profundos, donde la marca obstaculizada llega más tarde, y en el Estrecho de Cádiz, donde ocurre primero debido a la propagación del movimiento del mar Mediterráneo. Pasando de estas costas a las orillas americanas a través del Océano, llega primero a las costas más orientales de Brasil hacia la hora cuarta o quinta, después a las bocas del Amazonas a la hora sexta, pero a las islas adyacentes a la hora cuarta; después a las Islas Bermudas a la séptima y al puerto de San Agustín en Florida a la hora séptima y media. Por consiguiente pasa la marea a través del Océano más lentamente que en razón del paso de la Luna y bien necesario que es este retraso, para que al mismo tiempo el mar descienda entre Brasil y Nueva Francia y ascienda en las Canarias y las costas de Europa y África, y viceversa. Pues el mar no puede subir en un lugar sin bajar al mismo tiempo en otro. Es verosímil que en el Pacífico el mar se mueva también según la ley ya expuesta. Pues dicen que en las costas de Chile y Perú una marea muy alta coincide con la hora tercia lunar; pero aún no he podido determinar con qué velocidad se propaga desde allí hasta la costa oriental de Japón y hasta las Filipinas, y demás islas adyacentes al reino de China.

45. Diferentes fenómenos se originan por los obstáculos de las cuencas marinas y de las costas; hasta el punto que el mar solo suba una vez cada día

Además puede ocurrir que la marea se propague desde el océano por distintos estrechos hacia el mismo puerto, y pase primero por unos estrechos que por otros: en cuyo caso la misma marea, dividida en dos o más llegadas sucesivas podría componer movimientos nuevos de diversa índole. Supongamos que la marea se divide en dos iguales, de las cuales la primera antecede a la segunda en seis horas, y coincide con la hora tercia o la vigésimo séptima después del paso de la Luna sobre el meridiano del puerto. Si la Luna en este paso concreto por el meridiano se hallase en el Ecuador, los flujos llegarán con ondulaciones iguales en cada seis horas; las cuales, al coincidir con los respectivos reflujos, se igualarán con los flujos y así harán que en el espacio de tal día el agua esté tranquilamente estancada. Pero si en aquel momento la Luna estuviese declinada del Ecuador, las olas serán en el océano mayores y menores alternativamente, como se ha dicho, y por tanto se propagarán hacia el puerto alternativamente dos mayores y dos menores. Los dos flujos mayores componen una ola muy alta en el punto medio entre ambos; el flujo mayor y menor harán que el agua suba hasta el punto medio entre ambos; y entre los dos flujos menores el agua alcanzará la altitud mínima. Así, en el espacio de veinticuatro horas el agua alcanzará la máxima altura no dos veces como suele ocurrir, sino una sola; y una sola también la mínima; y la altura máxima, si la Luna declina hacia el polo suprahorizonte, ocurrirá o en la hora sexta o en la trigésima desde el paso de la Luna por el Meridiano; y al cambiar la declinación de la Luna, cambiará hacia el reflujo. De todo lo cual tenemos un ejemplo en el puerto de Batshaw en el reino de Tonquin, con latitud boreal de 20º 50’. Allí el agua, al día siguiente del paso de la Luna por el Ecuador, se estanca: después, al declinar la Luna hacia el Norte, empieza a fluir y refluir, no dos veces como en otros puertos, sino una vez cada día; y la pleamar coincide con el ocaso de la Luna y la bajamar con el orto lunar: al aumentar la declinación de la Luna aumenta esta marea hasta el día séptimo u octavo; después durante otros siete días decrece con los mismos pasos con que antes había crecido; y, al cambiar la declinación de la Luna, cesa y más tarde se convierte en reflujo. Pero desde ese momento, el reflujo coincide con el ocaso de la Luna y el flujo con el nacimiento hasta que la declinación cambie de nuevo. La entrada del océano a este puerto es doble: una más corta y recta entre la isla de Hinan y las costas de Quantum, provincia de China; la otra rodeando la dicha isla por frente o las costas de Cochinchina. Por el más corto la marea se propaga primero hasta Batshaw.

46. Los tiempos de las mareas son más irregulares en los canales de los ríos que en el océano.

En las cuencas de los ríos depende el flujo y reflujo del curso de los ríos. Pues dicho curso hará que el agua suba más lentamente desde el mar o que refluya más rápida y velozmente hacia el mar y también que tarde más en refluir que en fluir, sobre todo si sube mucho río arriba donde la fuerza del mar es menor. Así en el río Avon, tres hitos más abajo de Bristol dice Sturmy que el agua sube durante cinco horas y baja durante siete; más arriba de Bristol hacia Caresham o Bath la diferencia es sin duda mayor. También depende esta diferencia de la magnitud del flujo y del reflujo. Pues en las Sicigias de los astros el movimiento más fuerte del mar superando más fácilmente la resistencia del río hará que el agua crezca más rápidamente y durante más tiempo, y por tanto disminuirá está diferencia. Pero además, mientras la Luna pasa por las Sicigias, es preciso que los ríos, debido o que sus corrientes se encuentren obstaculizadas por el volumen de la marea, se llenen más y por tanto impidan algo más el reflujo del mar inmediatamente después de las Sicigias que inmediatamente antes. Por esta causa las mareas más lentas no coinciden con las Sicigias, sino que las preceden un poco. Dije también que las mareas antes de las Sicigias se hacen más lentas por la fuerza del Sol. Únanse ambas causas y el retraso de las mareas será mayor, y precederá aún más o las Sicigias. Deduzco que todos estas cosas son así a partir de las tablas de mareas confeccionadas por Flamsteed tras muchas observaciones.

47. Las mareas de mares mayores y más profundos resultan mayores y también son mayores en las costas de los continentes que en las islas de en medio del mar, y mayores todavía en las ensenadas de playas bajas y abiertas a los océanos

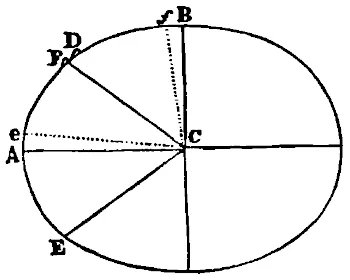
Por las leyes hasta aquí descritas se siguen los tiempos de las mareas. La magnitud depende de la magnitud del mar. Sea C el centro de la Tierra; sea EADB la figura oval del mar; CA el semieje mayor de esta figura oval. CB el semieje menor que cae sobre el anterior en ángulo recto; D el punto medio entre A y B, y ECF o eCf el ángulo central de la Tierra que contiene al mar que acaba en las costas E, F o bien e, f. Pongamos el punto A en medio entre E y F o el punto D entre e y f; y si por las diferencias de altura entre CA, CB representáramos la magnitud de la marea en un mar muy profundo que rodease toda la Tierra, el exceso de CA sobre CE o CF representará la magnitud de la marea en medio del mar EF comprendido entre las costas E, F; y el exceso de altura Ce sobre Cf representará muy aproximadamente la magnitud de la marea en las costas de dicho mar. De donde se desprende que las mareas en medio del mar son mucho menores que en las costas y que las marcas son en las costas muy similarmente a como la amplitud EF del mar es a un arco no mayor que el cuadrante. De aquí que en las inmediaciones del Ecuador donde el mar es estrecho entre África y América las mareas sean mucho más pequeñas que aquí en las zonas templadas, donde los mares se extienden abiertamente y que en las costas todas del Pacífico tanto americanas como chinas tanto dentro como fuera de los Trópicos; y que en las islas situadas en medio del mar apenas suban más de dos o tres pies, mientras que en las costas de los grandes continentes sean tres o cuatro veces mayores o aún más; sobre todo si los movimientos llegan desde un gran océano abierto y se van contrayendo poco a poco en un espacio angosto y el agua con gran fuerza y a través de lugares poco profundos esta obligada a llenar y vaciar alternativamente sinuosidades fluyendo y refluyendo. Como en Plymouth y en el puente de Chepstow en Inglaterra, como en el Mont S. Michael y en la ciudad de Auranches en Normandía, y en Camboya y Perú en las indias Orientales. En estos lugares el mar subiendo y bajando con gran velocidad ya inunda el litoral ya deja arenales de muchas millas, y la fuerza del flujo y del reflujo no puede pararse antes de que el agua suba o baje 40, 50, o más pies, y así los estrechos largos, poco profundos y abiertos a los océanos con bocas más anchas y profundas que el resto del estrecho, de cuya clase son el Británico y el de Magallanes en su entrada oriental, fluyen y refluyen más o aumenta y disminuye la corriente; y por esta razón suben y bajan más. Se dice que en las costas de América del Sur el Mar Pacífico algunas veces en su reflujo retrocede hasta dos millas y parece huir de quien está en la costa. De donde también allí las mareas serán mayores. En aguas más profundas, en cambio, siempre es menor la velocidad del flujo y del reflujo y por tanto también menor la subida y la bajada. En semejantes lugares el océano, que se sepa, no sube más de seis, ocho o diez pies. La cantidad pues del ascenso la mido así.

48. De los principias expuestos se calcula la fuerza del Sol para perturbar los movimientos de la Luna

Sea S el Sol; T la Tierra; P la Luna; PADE la órbita de la Luna. Tómese sobre SP el segmento SK igual a ST, y SL a SK en razón cuadrada de SK a SP, y trácese LM paralela a PT; y si la fuerza media circumsolar que actúa sobre la Tierra se representa por ST, o por SK, será SL la fuerza circumsolar que actúa sobre la Luna. Esta se compone de las partes SM, LM, de las cuales LM perturba el movimiento de la Luna (como se expuso en la Prop. LXVI y sus Corolarios). En tanto que la Tierra y la Luna giran entorno a un centro común de gravedad, la Tierra estará influenciada por fuerzas equiparables; pero las sumas tanto de las fuerzas como de los movimientos es posible referirlas a la Luna y representar las sumas de las fuerzas y de los movimientos por las líneas TM y ML análogas a ellas. La fuerza ML en su valor medio es la fuerza con que la Luna puede girar en su órbita en torno a la Tierra en reposo a la distancia PT en razón cuadrada de los tiempos periódicos de la Luna en torno a la Tierra y de la Tierra en torno al Sol (por el Cor. 17 de la Prop. LXVI), esto es, en razón cuadrada de 27 días, 6 horas, 43 minutos a 365 días, 6 horas y 9 minutos, o sea como 1000 a 178 725, o también 1 a 178. La fuerza, con que la Luna puede girar en torno a la Tierra en reposo en su órbita a la distancia PT de 60 semidiámetros terrestres, es a la fuerza con la que en el mismo tiempo puede girar a la distancia de 60 semidiámtros como 60 a 60; y esta fuerza es a la fuerza de la gravedad entre nosotros como 1 a 60 × 60. Y por tanto el valor medio de la fuerza ML es a la fuerza de la gravedad en la superficie de la Tierra como 1 × 60 a 60 × 60 × 60 × 178, o sea como 1 a 638 092,6. De donde viene dada también la fuerza TM, de la proporción de las líneas TM, LM. Estas son las fuerzas del Sol por las que son perturbados los movimientos de la Luna.

49. Se calcula la fuerza del Sol para mover el mar

Si se desciende de la órbita de la Luna a la superficie terrestre, disminuirán estas fuerzas en razón de las distancias 60 a 1; y por tanto ahora la fuerzo ML se hará 38 604 600 veces menor que la fuerza de la gravedad. Esta fuerza, actuando sobre la Tierra por todas portes igual, apenas o casi apenas producirá cambio en el movimiento del mar, y por tanto puede despreciarse en la explicación de sus movimientos. La otra fuerza TM, en los lugares en que el Sol se sitúa en el zenit o en el nádir es tres veces mayor que la fuerza ML y por tanto 12 868 200 veces menor que la fuerza de lo gravedad.

50. Calcúlese la altura de la marea en el Ecuador resultante de la fuerza del Sol

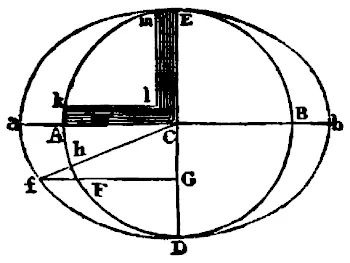
Representen, ahora ADBE la superficie esférica de la Tierra; aDbE al agua que lo cubre; C al centro de ambas, A el lugar sobre el que el Sol cae perpendicularmente, B el lugar opuesto; D, E los lugares distantes del anterior noventa grados; ACE, mlk un canal cilíndrico rectangular que pasa por el centro de la Tierra. La fuerza ML en cada punto es como la distancia desde él hasta el plano DE al cual es perpendicular la recta AC; y por ello en la parte EClm del canal es nula; y en la otra parte AClk es como la gravedad en cada una de las alturas. Pues la gravedad, en el descenso al centro de la Tierra es en cualquier sitio como la altura (por la Prop. LXXIII). Por consiguiente, la fuerza ML, al empujar el agua hacia arriba, disminuye su gravedad en una determinada proporción a lo largo del brazo AClk del canal. Y por ello el agua de este brazo del canal asciende para compensar con una mayor altura la falta de gravedad; y no reposará en equilibrio hasta que la gravedad total sea igual a la gravedad total en el brazo ClmE del canal. Puesto que la gravedad de una partícula cualquiera es como su distancia al centro de la Tierra, el peso total del agua en el brazo del canal crece como el cuadrado de la altura; y por tonto la altura del agua en el brazo Aclk será a la altura del agua en el brozo ClmE como la raíz cuadrada de la razón de los números 12 868 201 a 12 868 200; o en razón del número 25 623 053 al número 25 623 052, y la altura en el otro brazo EClm a la diferencia de alturas como 25 623 031 a 1. Es pues la altura de dicho brazo EClm de 19 615 800 pies parisinos, como ha sido recientemente establecido por los franceses; y en consecuencia, por la proposición dicha se sigue una diferencia de 9 pulgadas de dicho pie. Por tanto la altura del mar por causa de la fuerza del Sol será mayor en A que en E en unas nueve pulgadas[10] y aunque en el canal ACEmlk el agua se congele y quede rígida, permanecerán, no obstante, las alturas de las aguas que sobrenadan a la Tierra en A y en E y en todos los lugares intermedios.

51. Se calcula la altura de la marea en los paralelos debida a la fuerza del Sol

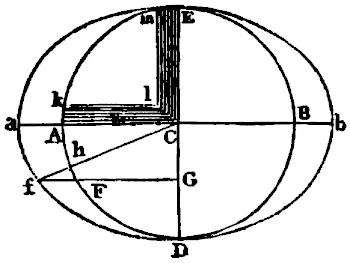
Represente Aa el exceso susodicho de nueve pulgadas de altura en a; y bf el exceso de altura en otro punto cualquiera b: Trácese la perpendicular fG sobre DC, que corte a la esfera en F. Dada la gran distancia al Sol, que hace que todas las líneas que se dirigen a él puedan considerarse paralelas, la fuerza TM en cualquier lugar b o f es a dicha fuerza en A como el seno FG al radio AC; y por tanto toda vez que dichas fuerzas tienden al Sol según líneas paralelas, generarán alturas paralelas Pf, Aa en la misma proporción. Y por tanto la figura del agua DfaEb será una esferoide, construida por la revolución de una elipse sobre su eje mayor ab. Así pues la altura perpendicular fb es a la altura oblicua fF como fG a fC o FG o AG; y por tanto la altura fb es a la altura Aa en razón cuadrada de FG a AG; esto es, en la razón que guardan el seno verso del doble del ángulo DCf al doble del Radio, y por tanto está dada. Y por esto, durante el aparente giro del Sol en torno a la Tierra, obtenemos en cada momento y en cada lugar en el Ecuador la tasa de ascenso y descenso. Se obtiene también el decrecimiento de la marea derivado tanto de la latitud de los lugares como de la declinación del Sol. Efectivamente de la latitud de los lugares, porque el ascenso y descenso del mar en cada lugar disminuye en razón cuadrada del seno del complemento de la latitud; y de la declinación del Sol, pero semejante ascenso y descenso en el Ecuador disminuye en razón cuadrada del seno del complemento de la declinación; y fuera del Ecuador la semisuma de los ascensos matutino y vespertino, esto es el ascenso medio, disminuye muy aproximadamente en la misma proporción.

52. La razón de las mareas del Ecuador en las Sicigias y en las Cuadraturas a partir de la fuerza del Sol, y de la Luna conjuntamente

Sean S y L las fuerzas del Sol y de la Luna situados en el Ecuador y a la distancia media de la Tierra. Sea R el radio; T y U los senos versos del doble de los ángulos complemento de la declinación del Sol y de la Luna en un momento dado; D y E los diámetros medios aparentes del Sol y de la Luna; F y G sus diámetros aparentes en dicho momento dado; y serán las fuerzas que produzcan las mareos en el Ecuador, en las Sicigias:

y en las Cuadraturas:

Si se observase en los paralelos la misma proporción de mareas, tendremos por las observaciones, realizadas con toda precisión en nuestra región boreal, la proporción entre las fuerzas L y S. Y finalmente con esta regla se podía predecir la magnitud de las mareas en cada Sicigia y en cada Cuadratura.

53. Cálculo de la fuerza lunar causante de las mareas y de la altura del agua resultante de ella

En la desembocadura del río Avon tres millas más abajo de Bristol, en primavera y otoño, el ascenso del agua, en la conjunción y oposición de Sol y Luna, es de 45 pies, según observaciones de Samuel Sturmy; mientras que en las Cuadraturas es solo de 25. Supongamos que los diámetros aparentes, que aquí no se establecen, son los diámetros medios; y también que la declinación de la Luna en las Cuadraturas equinocciales es la declinación media, esto es de 23 grados; entonces el seno verso del doble del ángulo complemento será de 1682, supuesto un radio de 1000. Por otro lado, la declinación del Sol en los equinoccios y la de la Luna en las Sicigias es nula; y el seno verso del doble del ángulo complemento es 2000. De aquí que la fuerza sea en las Sicigias de L + S y en las Cuadraturas de:

proporcional a las alturas de las mareas de 45 y 25 pies o de 9 y 5 pasos. Y multiplicados entre sí medios y extremos será:

o también

Recuerdo haber oído, por lo demás, que en verano el ascenso del mar en las Sicigias es al ascenso en las Cuadraturas casi como 5 a 4. En los mismos solsticios es verosímil que la proporción sea un poco menor, como de 6 a 5. De aquí se sigue que . Hasta que conste por las observaciones algo más cierto asumamos que ; y puesto que las mareas son como las fuerzas, la fuerza solar empujará a la marea a nueve pulgadas de altura y la de la Luna la empujará a cuatro pies. Supongamos que dicha altura, por la fuerza de reciprocación de las aguas por la que el movimiento una vez impreso se conserva un cierto tiempo, se duplica o tal vez se triplica; y se originará la magnitud total de la marea que de hecho se observa en los océanos.

54. Estas fuerzas del Sol y de la Luna solo se pueden observar mediante las mareas del mar

Bastan pues estas fuerzas para el movimiento del mar: pero además no producen, en cuanto yo puedo advertir, ningún otro efecto sensible en esta Tierra, pues dado que mediante una balanza sumamente exacta no es posible advertir un grano en una pesada de 4000 granos, y por otra parte la fuerza solar es 12 868 200 veces menor que la de la gravedad en orden a producir las mareas y la suma de las fuerzas del Sol y de la Luna, aun siendo mayor en razón de 6 a 1, es 2 032 890 veces menor que la de la gravedad, está claro que juntas dichas fuerzas son quinientas veces menores que aquellas que pudieran hacer aumentar o disminuir de modo sensible el peso de un cuerpo cualquiera, pesado en una balanza. De donde ni siquiera en los experimentos de péndulos, de barómetros, colocados sobre agua en reposo, y procedimientos estáticos similares, han dado como resultado efectos sensibles. Ciertamente la atmósfera fluye y refluye por estas fuerzas de modo semejante al mar, pero con un movimiento tan pequeño que de él no se sigue el más mínimo viento sensible.[11]

55. El cuerpo de la Luna es casi seis veces más denso que el del Sol

Si se igualasen entre sí tanto los efectos del Sol y de la Luna para producir las mareas como sus diámetros aparentes, serían sus fuerzas absolutas como las magnitudes (por el Corolario 14 de la Proposición LXVI). Pero el efecto lunar es al efecto del Sol como 5 a 1 aproximadamente; y el diámetro es menor en razón de 31 a 32, o de 45 a 46. Hay que aumentar pues la fuerza de la Luna directamente en la razón del efecto e inversamente en el cubo de la razón del diámetro: y de este modo la fuerza de la Luna referida a su magnitud será a la fuerza del Sol referida también a su magnitud como 5 a 1 e inversamente a la razón cúbica de 45 a 46, esto es casi como 5 a 1. La Luna tiene, pues, una fuerza centrípeta absoluta en razón a su magnitud como 5 a 1 mayor que el Sol respecto a la suya, y por tanto es también más densa en la misma proporción.

56. La Luna es más densa que nuestra Tierra en razón casi de 3 a 2

En el tiempo de 27d 7h 43' en que gira la Luna en torno a la Tierra, un planeta a la distancia de 18 954 diámetros solares desde el centro del Sol puede girar en torno al mismo, supuesto que el diámetro medio aparente del Sol es de 32' . En este tiempo la Luna puede girar en torno a la Tierra en reposo a la distancia de 30 diámetros terrestres. Si fuese el mismo el número de diámetros en uno y otro caso, la fuerza absoluta circumterrestre sería a la fuerza absoluta circumsolar como la magnitud de la Tierra a la magnitud del Sol (por el Cor. 2 de la Prop. LXXII). Puesto que los diámetros terrestres son más en razón de 30 a 18 954, el cuerpo terrestre será menor en dicha razón al cubo, esto es en razón de 3 a 1. Es por tanto la fuerza de la Tierra en función de su tamaño respecto a la del Sol en función del suyo como 3 a 1; y por tanto la densidad de la Tierra a la densidad del Sol en la misma proporción. Puesto que la densidad V de la Luna es respecto a la densidad del Sol como 5 a 1, sera la densidad de la Luna a la de la Tierra como 5 a 3, esto es como 23 a 16. De donde, dado que la magnitud de la Luna es a la magnitud de la Tierra como 1 a 41 aproximadamente, la fuerza centrípeta absoluta de la Luna será a la fuerza absoluta de la Tierra como 1 a 29 aproximadamente; y asimismo la cantidad de materia en la Luna y la cantidad de materia en la Tierra estarán en la misma proporción. De aquí se obtiene el centro común de gravedad de la Luna y la Tierra más exactamente que antes: conocido este será posible calcular con mayor exactitud la distancia de la Luna a la Tierra. Pero prefiero esperar hasta que la proporción entre los cuerpos de la Luna y la Tierra entre sí sea conocida más exactamente a partir de los fenómenos de las mareas; esperando también mientras tanto que acontezca que la circunferencia de la Tierra sea medida desde mayores intervalos entre estaciones de lo que hasta ahora se ha hecho.

57. Sobre la distancia de las fijas

Hasta aquí he expuesto el sistema de los planetas. Pero de la falta de paralaje anual se sigue que las estrellas fijas distan de dicho sistema intervalos inmensos. Es muy cierto que dicha paralaje es menor de un minuto, y por tanto las distancias de las fijas superan a la distancia de Saturno al Sol más de 360 veces. Quienes adscriben la Tierra a los planetas y el Sol a las estrellas fijas, alejarán a estas aún más con los argumentos siguientes. Del movimiento anual de la Tierra debe surgir una translocación de las fijas entre sí, aproximadamente igual al doble de la paralaje. Pero las estrellas mayores y más cercanas respecto a las lejanas y que solo se alcanzan a ver con el telescopio, no se observa en absoluto que se muevan. Supongamos que su movimiento sea menor que 20", y la distancia de las fijas más cercanas superará a la distancia media de Saturno 2000 veces. Ahora bien, Saturno con su disco de 17" o 18" de ancho recibe aproximadamente 1/2 100 000 000 de la luz solar. Pues tanto menor es dicho disco que la superficie total esférica de Saturno. Si se supone que Saturno refleja como la cuarta parte de esta luz, la luz total que se refleja desde el hemisferio iluminado vendrá a ser de 1/4 200 000 000 parte de la luz dimanante del hemisferio Solar. Luego habida cuenta de que la luz se enrarece en razón al cuadrado de la distancia del cuerpo que luce, si el Sol estuviese veces más distante que Saturno, se vería desde aquí igual de brillante que se ve Saturno sin su anillo; y por tanto sería poco más brillante que una estrella fija de primera magnitud. Pongamos pues que la distancia a que luciese el Sol como estrella fija fuese 100 000 veces mayor que la distancia de Saturno y su diámetro aparente sería de 7””', 16””” y la paralaje debida al movimiento anual de la Tierra sería de 13””. Y tal sería la distancia, el diámetro aparente y la paralaje de las estrellas fijas iguales a nuestro Sol en tamaño y luz. Alguien juzgará legítimo suponer que gran parte de la luz de las estrellas fijas en su paso por tan grandes espacios es detenida y desaparece, y, por tonto que se deberían acercar más las estrellas fijas; aunque por esta razón las fijas más distantes apenas si podrían verse. Supongamos, por ejemplo, que las tres cuartas partes de la luz desaparecen en el tránsito desde las estrellas fijas más próximas hasta nosotros, y por segunda vez perderá tres cuartas partes en el tránsito por un espacio doble del anterior y lo mismo por tercera vez en un espacio triple y así sucesivamente; por tanto las estrellas fijas que estén el doble más lejos serán 16 veces más oscuras; a saber: cuatro veces más oscuros por la disminución del diámetro aparente y, además, cuatro veces más oscuras por la pérdida de luz: y por el mismo argumento las fijas tres veces más distantes serán 9 × 4 × 4 esto es 144 veces más oscuras; y las que estén cuatro veces más lejos serán 16 × 4 × 4 × 4 esto es 1024 veces más oscuras. Semejante disminución de luz no concuerda en nada con los fenómenos ni con la hipótesis de que las fijas están a distancias distintas.

58. Que los cometas, cuando aparecen a la vista, están más cerca que Júpiter se prueba a partir de la paralaje longitudinal

Distando pues entre sí los astros tan grandes intervalos ni se atraen sensiblemente entre sí, ni son atraídos por nuestro Sol. Pero es necesario que los cometas estén sometidos a la fuerza circumsolar; ya que si la falta de paralaje diurna los coloco fuera de las regiones sublunares, del mismo modo la paralaje anual arguye en favor de su descenso a las regiones planetarias. Porque todos los cometas que marchan según el orden de los signos, al final de la aparición, son más lentos de lo normal o retrógrados si la Tierra está entre ellos y el Sol; pero también son más rápidos si la Tierra camina en oposición. Y por el contrario, los que corren en dirección contraria al orden de los signos, son precisamente más rápidos al final de la aparición, si la Tierra camina entre ellos y el Sol; y más lentos o retrógrados si la Tierra está situada en la parte opuesta. Acontece esto de modo muy distinto según el diferente lugar en que se produzca el movimiento de la Tierra. Si la Tierra se dirige hacia el mismo sitio que el cometa y va más deprisa, el cometa será retrógrado, si va más despacio será al menos más lento; y cuando la Tierra marcha en sentido contrario, será más rápido. Calculando las diferencias entre movimientos más rápidos y más lentos y las sumas de los movimientos más rápidos y de los retrógrados y comparándolas con la situación y el movimiento de la Tierra de los cuales se derivan, encuentro que, por esta paralaje, la distancia de los cometas en el tiempo en que son observables a simple vista es siempre menor que la distancia de Saturno y las más de las veces menor que la distancia de Júpiter.

59. Se prueba por la paralaje en latitud.

Lo mismo se deduce de la curvatura del camino de los cometas. Caminan estos cuerpos casi en círculos máximos, mientras se mueven más rápidamente; pero al final del recorrido, cuando el movimiento aparente derivado de la paralaje tiene mayor proporción con respecto al movimiento total aparente, suelen apartarse de dichos círculos; y cuantas veces la Tierra se mueve en una dirección, se dirigen hacia la opuesta. Se origina esta desviación, sobre todo, de la paralaje por cuanto responde al movimiento de la Tierra; y la gran magnitud de aquella, según mis cálculos, sitúa a los cometas que se alejan bastante por debajo de Júpiter. De donde se sigue que en los perigeos y perihelios, cuando están más cerca, muchas veces descienden por debajo de las órbitas de Marte y de los planetas inferiores.

60. Se prueba de otro modo por la paralaje

. Además se confirma tamaña cercanía por la paralaje de la órbita anual en tanto en que esta se calcula muy aproximadamente a partir de la hipótesis de que los cometas se mueven uniformemente en líneas rectas. Es conocido ya el método (intentado por Kepler y perfeccionado por Wallis y Wren) de calcular la distancia de un cometa según esta hipótesis a partir de cuatro observaciones: y los cometas reducidos a esta regularidad suelen atravesar por medio de la región planetaria. Como los cometas de 1607 y 1618 entre el Sol y la Tierra, según lo determinó Kepler, el de 1664, bajo la órbita de Marte; y este de 1680, bajo la órbita de Mercurio, según determinaron Wren y otros. En virtud de tal hipótesis rectilínea Hewelcke situó a todos los cometas observados de que hay constancia bajo la órbita de Júpiter. Yerran por tanto y hablan sin cálculos astronómicos quienes, a partir del movimiento regular de los cometas, o los alejan hasta la región de las fijas, o niegan el movimiento de la Tierra; puesto que no pueden reducirse sus movimientos a total regularidad, salvo admitiendo su paso por regiones cercanas a la Tierra. Y estos son los argumentos que se basan en la paralaje, en la medida en que esta puede determinarse sin un conocimiento exacto de las órbitas y movimientos de los cometas.

61. Por la luz de las cabezas se prueba que los cometas bajan hasta la órbita de Saturno

Se confirma también la proximidad de los cometas por la luz de las cabezas. Pues el brillo de un cuerpo celeste iluminado por el Sol y que se aleja hacia regiones distantes disminuye en razón de la cuarta potencia de la distancia; en razón cuadrada por el aumento de la distancia al Sol, y en otra razón cuadrada por la disminución del diámetro aparente. De aquí se sigue que Saturno, por el doble de distancia y la mitad casi de diámetro aparente que Júpiter debe parecer 16 veces más oscuro que este; y que si la distancia fuese cuatro veces mayor, su luz sería 256 veces menor y por tanto apenas podría verse a simple vista. Los cometas, en cambio, no es raro que igualen con su luz a la de Saturno, aunque no lo superen en diámetro aparente. El cometa de 1678, según las observaciones de Hooke, igualaba con su luz a las fijas de primera magnitud; y su cabeza, o estrella central del cometa, vista a través de un telescopio de quince pies, aparecía igual en brillo que Saturno sobre el horizonte; pero el diámetro de la cabeza era solamente de 25", esto es el mismo casi que el diámetro de un círculo igual a Saturno junto con el anillo. El círculo de la cabellera del cometa en torno a la cabeza del mismo era unas diez veces mayor, a saber 4 minutos. Además, el diámetro mínimo de la cabellera del cometa de 1682, observado por Flamsteed con un tubo de 16 pies y medido mediante micrómetro, era igual a 2‘0“. El núcleo en cambio, o estrella central, apenas ocupaba la décima parte de esta anchura y, por tanto, tenía de ancha solo 11“ o 12“. Sin embargo superaba en luminosidad al cometa de 1680 y emulaba a las estrellas de primera y segunda magnitud. Añádase que el cometa de 1665, como refiere Hewelcke, en abril superaba en claridad a casi todas las fijas, y hasta al mismo Saturno, en razón a su color mucho más vivido, puesto que era mucho más brillante este cometa que el otro que había aparecido a finales del año anterior y era comparado con estrellas de primera magnitud. La anchura de la cabellera era de 6‘ aproximadamente, mientras el núcleo, comparado con los planetas por medio del tubo óptico, era claramente menor que Júpiter y, a veces, era igual que el solo cuerpo central de Saturno, a veces, igual al mismo. Añádase el anillo y la cara visible de Saturno aumenta al doble, pero la luz no será más intensa que la del cometa: por tanto el cometa estaba más cerca del Sol que Saturno. De la proporción entre núcleo y cabellera puesta en claro por estas observaciones y de la anchura que raramente supera los 8‘ o 12‘ se infiere que las estrellas de los cometas a lo sumo serán de la magnitud de los planetas; en cambio la luz frecuentemente puede compararse con la de Saturno, e incluso a veces superarla. Y, por tanto, sus distancias en los perihelios apenas serán mayores que la de Saturno. A doble distancia la luz habría de ser cuatro veces menor y por el oscurecimiento del brillo tendría que disminuir respecto a la luz de Saturno tanto como la luz de este disminuye respecto a la de Júpiter: diferencia que podría observarse fácilmente. A distancia diez veces mayor, sus cuerpos superarían al cuerpo del Sol mientras su luz disminuiría cien veces respecto a la de Saturno. Y a distancias mayores tales cuerpos superarían ampliamente al Sol, y situados en las profundidades tenebrosas ya no se distinguirían. Tan lejos lleva el que, considerando a nuestro Sol entre las fijas, sean alejados los cometas a las regiones intermedias entre el Sol y las fijas. Ciertamente, allí no deberían ser iluminados por el Sol, más de lo que nosotros somos iluminados por la mayor de las estrellas fijas.

62. Que descienden bastante bajo la órbita de júpiter, y a veces bajo le órbita de la Tierra

Hemos discutido todo esto sin considerar el oscurecimiento de los cometas por causa del humo muy abundante y opaco que rodea a la cabeza, la cual brilla siempre dificultosamente como a través de una nube. Pues cuanto más oscuro se torna un cuerpo por causa de este humo, tanto más necesario es que se acerque al Sol para que la cantidad de luz, que de sí refleje, emule o la de los planetas. Por tanto se hace verosímil que los cometas desciendan largamente bajo la órbita de Saturno, como probamos por la paralaje. Esto mismo se confirma muy bien por las colas. Estas se originan o de la reflexión del humo difuso por el éter, o de, la luz de la cabeza. En el primer caso hay que disminuir la distancia de los cometas, para que el humo, que siempre sale de la cabeza, no se propague por espacios demasiado amplios con velocidad y expansión increíbles. En el segundo caso toda la luz, tanto de la cabellera como de la cola ha de adscribirse al núcleo de la cabeza. Pero si se llega a imaginar que se reúne toda esa luz y se encierra dentro del disco del núcleo, tal núcleo ciertamente, cada vez que emita una cola máxima y muy resplandeciente, superará con mucho o Júpiter con su resplandor. Por tanto con un diámetro aparente menor y emitiendo más cantidad de luz, estará mucho más iluminado por el Sol y en consecuencia estará mucho más cerca del mismo. Así el cometa del año 1679, del 12 al 15 de diciembre del antiguo calendario, en cuyo tiempo emitía una cola muy luminosa y no dispar o la luz difusa y dispersa por tan grandes espacios de muchos Júpiter, en cuanto a la magnitud del núcleo (como observaba Flamsteed) era menor que Júpiter, y como consecuencia mucho más cercano al Sol. Es más, era menor que Mercurio; pues el 27 de dicho mes, cuando más cerca estaba de la Tierra, le pareció a Cassini, a través de un telescopio de 35 pies, un poco más pequeño que el globo de Saturno. El día ocho de dicho mes, al amanecer vio Halley una cola muy corta y ancha y como si saliese del cuerpo del Sol a punto de nacer y parecida a una nube extraordinariamente brillante, y no desapareció hasta que el propio Sol no empezó a verse sobre el horizonte. Superaba pues este resplandor la luz de las nubes hasta el nacimiento del Sol, y cediendo solamente ante el resplandor inmediato del Sol, superaba ampliamente a la luz de todas las estrellas juntas. No suelen verse Mercurio, ni Venus ni la propia Luna cuando están tan cerca del Sol. Supongamos que toda esta luz dispersa se reúne y se encierra en el núcleo de un cometa menor que Mercurio; y con un brillo hecho ahora más fuerte será más visible, superará largamente a Mercurio y será más cercano al Sol. Durante los días 12 y 15 de dicho mes, esta cola, esparcida por espacios muchos más amplios, apareció más rarificada; pero la luz, no obstante, era tan fuerte que se podía ver cuando las estrellas fijas apenas eran visibles; después exhibió una especie de estela que brillaba de modo maravilloso. Corríjase la luminosidad total de una longitud de cuarenta a cincuenta grados y de una latitud de dos.

63. Se prueba lo mismo a partir del gran resplandor de las colas en las inmediaciones del Sol

Se confirma semejante acercamiento de los cometas al Sol por el sitio donde brillan en mayor grado. Pues al pasar la cabeza por el Sol y todavía permaneciendo bajo los rayos solares es cuando han sido descritas las colas más brillantes de todas y como si saliesen del horizonte en forma de estelas de fuego; después, al venir a la vista la cabeza y al apartarse del Sol, el brillo disminuye siempre y se hace semejante a la palidez de la Vía Láctea, aunque al principio mucho más brillante para después acabar languideciendo. Así era aquel resplandeciente cometa descrito por Aristóteles en el Lib. I, 6 de los Meteoros cuya cabeza no se vio el primer día ya que había caído delante o al menos bajo los rayos solares; pero al día siguiente fue visible por completo, «pues dejó el Sol a la menor distancia posible y se situó inmediatamente detrás». Por el enorme brillo de la cola, no aparecía aún el fuego disperso de la cabeza, pero «pasado el tiempo (dice Aristóteles) como (la cola) brillase ya menos volvió a verse la cara de (la cabeza) del cometa. Y extendió su resplandor hasta la tercera parte del cielo (esto es hasta 60 grados). Apareció en invierno y ascendió hasta el cinturón (de Orión) donde desapareció». Justino en el Lib. 37 describe dos cometas del mismo género, los cuales, dice, lucieron de tal modo «que parecía que ardiera todo el cielo y que ocupasen con su tamaño la cuarta parte del cielo y con su resplandor vencieran al del Sol». Con estas últimas palabras se insinúa la yuxtaposición del brillo del cometa y de Sol naciente o poniente. Añádase el cometa del año 1101 o de 1106 cuya estrella era pequeña y oscura, como aquella del año 1680, «pero el resplandor, que salió de ella, muy brillante y como una inmensa estela que se dirigía al Oriente y al Norte» como dice Hewelcke citando a Simeón monje de Durham; apareció al principio del mes de Febrero por la tarde sobre el ocaso suroeste del Sol. De ello y de la situación de la cola podemos inferir que la cabeza estaba cercana al Sol. «Distaba del Sol, dice Mateo de París, como un codo, emitiendo de sí un largo rayo desde la hora tercia (mejor sexta) hasta la hora nona». El cometa del año 1264, en el mes de julio, o alrededor del Solsticio, precedía al Sol naciente, emitiendo sus rayos con una gran luminosidad hasta la mitad del cielo hacia Occidente. Y al principio subía poco sobre el horizonte, pero, al avanzar el Sol, se alejaba cada día del horizonte, hasta que por fin atravesó la mitad del cielo. Dícese que al principio fue grande y luminoso, teniendo una cola larga, la cual, día a día, fue decreciendo. Es descrito en el Apend. de Mateo de París. Hist. Angl. de este modo: «El año de C. de 1265 apareció un cometa tan notable como nadie de los entonces vivos había visto antes, pues saliendo desde el oriente con gran resplandor, se extendía con gran brillo hasta la mitad del hemisferio hacía occidente». El año 1401 o 1402, hundido ya el Sol bajo el horizonte, apareció en Occidente «un cometa luminoso y brillante, mostrando una cabellera enhiesta y como de fuego llameante, no muy distinta de una lanza emitiendo rayos desde el ocaso hacia el oriente; desde el Sol, hundido bajo el horizonte, iluminaba con los efluvios de sus rayos todas las regiones de los límites de la Tierra, y no permitía a las demás estrellas emitir su luz, ni a las noches oscurecer con sombras la atmósfera, por cuanto que su luz, vencía al resplandor de los otros y se extendía flameando hasta el vértice del cielo mientras estaba sobre el horizonte», etc. Hist. Byzant. Duc. Niich. Nepote, cap. 16. Por la ubicación de la cola y por el tiempo de esta primera aparición, se sigue que la cabeza en aquel momento estaba en las inmediaciones del Sol y poco a poco se fue apartando de él; pues el tal cometa duró tres meses. El año 1527, el 11 de Agosto, hacia la hora cuarta de la mañana se vio en casi toda Europa un cometa terrible en Leo que duró luciendo una hora y cuarto cada día. Salió por el oriente, se dirigió hacia mediodía y ascendió hasta occidente con una longitud inmensa; en cambio fue hacia el septentrión donde fue más visible, y es descrito con una nube terrible (esto es la cola), teniendo, según la opinión del vulgo, la forma de un brazo curvado con una espada de tamaño descomunal. El año 1618, los últimos días de Noviembre, se extendió el rumor de que bajo la salida del Sol aparecía uno estela blanca, que resultó ser efectivamente la cola de un cometa, cuya cabeza todavía estaba brillante dentro de la claridad de los rayos solares. El 24 de noviembre y después se vio el cometa con luz nítida, con cabeza y cola brillantes. La longitud de la cola, que primero fue de 20 o 30 grados, creció hasta el 9 de diciembre, cuando llegó a alcanzar 75, pero con luz siempre más dispersa y difusa que al principio. El año 1668 el 5 de Marzo del nuevo calendario, a la hora séptima de la tarde, el padre Valentín Entancel, estando en Brasil, vio un cometa próximo al horizonte hacia el ocaso del Sol en el suroeste, de cabeza pequeña y apenas visible, pero con una cola de tal modo brillante que quienes estaban en el litoral fácilmente vieron su imagen reflejada en el mar. Tamaño resplandor solo duró tres días, y enseguida decreció notablemente; la cola al principio iba desde occidente hacia mediodía y casi paralela al horizonte, tenía la forma de estela luminosa de 23 grados de longitud. Después, al decrecer la luz aumentó el tamaño hasta que el cometa dejó de aparecer. Así, Cassini en Bolonia los días 10, 11 y 12 de Marzo lo vio salir del horizonte con una longitud de 32 grados. En Portugal, se dice que ocupaba casi la cuarta parte del cielo, esto es, casi 45 grados, con una enorme estela extendida de occidente a oriente muy brillante, pese a que no aparecía completa al estar ya siempre en estos lugares la cabeza brillando bajo el horizonte. Por el aumento de la cola está claro que la cabeza se ha apartado ya del Sol y que estuvo próxima a él al principio, cuando la cola brillaba en el mayor grado. Añádase a todo esto el cometa de 1680, cuyo enorme resplandor en su conjunción con el Sol ya he descrito antes. Tan gran resplandor arguye en favor de que los cometas de esta clase pasan en verdad por la fuente de la luz, sobre todo porque las colas jamás brillan así en oposición al Sol, ni se sabe que en tal situación hayan aparecido estelas ígneas.

64. Se prueba por la luz de las cabezas en tanto que, «caeteris paribus», es mayor en la cercanías del Sol

Finalmente lo mismo se sigue del hecho de que la luz de las cabezas crezca al apartarse los cometas de la Tierra hacia el Sol y mengue en su regreso desde el Sol hacia la Tierra. Así el último cometa del año 1665, según observó Hewelcke, desde que empezó a verse, disminuía en su movimiento y por consiguiente había pasado ya del perigeo; pero el brillo de la cabeza crecía día a día hasta el punto de que el cometa oscurecido por los rayos solares dejó de verse. El cometa de 1683, según observó el propio Hewelcke, a finales de julio, cuando se vio por primera vez, se movía muy lentamente recorriendo en su órbita 40 o 45 minutos cada día. A partir de estas fechas su movimiento diario aumentaba constantemente hasta el 4 de septiembre en que avanzó casi cinco grados, por tanto durante todo este tiempo se acercaba a la Tierra; esto mismo se deduce del diámetro de la cabeza medido con micrómetro, ya que Hewelcke halló que este era el 6 de Agosto de tan solo 6’5” incluida la cola y el 2 de Septiembre era de 9’7”. La cabeza por tanto aparecía al principio mucho menor que al final del movimiento; sin embargo al principio, en las cercanías del Sol era mucho más luminoso que hacia el final, como refiere el propio Hewelcke. Por tanto, durante todo este tiempo, debido a su receso respecto al Sol, disminuyó en luminosidad pese a su acercamiento a la Tierra. El cometa del año 1618, hacia mediados de Diciembre, y este de 1680, hacia finales del mismo mes, se movían muy velozmente, y por tanto estaban en esos momentos en los perigeos; pero el máximo brillo de las cabezas ocurrió casi dos semanas antes, apenas salidas de los rayos del Sol, y el máximo brillo de las colas un poco antes, en la máxima cercanía al Sol. El 12 de Diciembre, fue vista y observada por Flamsteed la cabeza de este último cometa a la distancia de nueve grados del Sol, cosa que escasamente podría concederse a una estrella de tercera magnitud. Los días 15 y 17 de Diciembre apareció como una estrella de tercera magnitud, si bien disminuido en su brillo nebular al estar situado junto al Sol. El 26 de Diciembre, moviéndose a gran velocidad y ya situado prácticamente en el perigeo, era menor que la «Boca de Pegaso» (Os pegasi), estrella de tercera magnitud; el 3 de Enero, parecía una estrella de cuarta magnitud, el 9 de Enero como de quinta; el 13 de Enero, debido al brillo de la Luna creciente, desapareció; en 25 de Enero apenas igualaba a las estrellas de séptima magnitud. En cambio la cabeza del cometa primero, según las observaciones de Cysat, el 1 de Diciembre parecía mayor que las estrellas de primera magnitud, y el 16 de Diciembre (situado ya en el perigeo), de pequeña magnitud había perdido mucho en brillo o en claridad de luz. Kepler, el 7 de Enero, inseguro ya sobre la cabeza del cometa, dejó de observarlo. Si se toman tiempos iguales antes y después del perigeo, las cabezas, situadas en regiones remotas, brillarían igual antes y después; y esto a causa de la igualdad de distancias a la Tierra. El que en un caso brillasen mucho y en el otro se desvanecieran debe atribuirse a la vecindad del Sol en el primero y a la distancia al mismo en el último. Y de tan gran diferencia de luz entre ellos se infiere la gran cercanía en el primero pues la luz de los cometas suele ser regular, y aparecer en toda su magnitud, cuando las cabezas se mueven a gran velocidad y están por tanto en los perigeos; salvo en la medida en que ella es mayor en las proximidades del Sol.

65. Se confirma esto por el gran número de cometas que se han visto en la región solar

Por esto he llegado a comprender al fin por qué frecuentan tanto los cometas la región del Sol. Si se considerasen en las regiones de más allá de Saturno, deberían aparecer más frecuentemente en las partes opuestas al Sol. Estarían pues más próximos a la Tierra los que se ubicasen hacia este lado, y la interposición del Sol oscurecería a los otros. Pero repasando la historia de los cometas, he encontrado que se han detectado cuatro o cinco veces más hacia el hemisferio solar que en el opuesto, además de otros, sin duda no pocos, que han ocultado la luz del Sol. Pues al descender hasta nuestras regiones, ni emiten colas, ni son iluminados tampoco por el Sol suficientemente como para que puedan ser vistos a simple vista antes de que estén más cerca que el mismo Júpiter. La mayor parte, pues, del espacio descrito con este pequeño intervalo en torno al Sol, está ubicada del lado de la Tierra que mira al Sol; y en dicha mayor parte, al estar muy cercanos al Sol, suelen estar más iluminados. Debido a la gran excentricidad de las órbitas ocurre que los ápsides inferiores estén mucho más cerca del Sol que si las revoluciones ocurrieran en círculos concéntricos al Sol.

66. Se confirma también por las colas mayores y más luminosas después de la conjunción de las cabezas con el Sol que antes

Por esto comprendemos también por qué las colas de los cometas, al aproximarse las cabezas al Sol, aparezcan siempre difusas y breves y se diga que apenas hayan sobrepasado 15 o 20 grados de longitud; mientras que en el receso de las cabezas desde el Sol, brillan frecuentemente como estelas ígneas y con frecuencia se extienden a lo largo de 40, 50, 60, 70 y más grados de longitud. Efectivamente, se origina tamaño brillo de las colas y semejante longitud debido al calor solar que calienta al cometa al pasar este y me parece que de aquí se desprende que todos los cometas con colas semejantes han pasado por las cercanías del Sol.

67. Las colas se originan de la atmósfera de los cometas

También es posible desprender de aquí que las colas se originen de la atmósfera de las cabezas. Tres son las opiniones sobre las colas: o que es el resplandor del Sol propagado a través de la cabeza transparente del cometa; o que se origina de la refracción de la luz en su propagación desde la cabeza del cometa hasta la Tierra; o bien, finalmente, que se trata de una nube o vapor que surge continuamente de la cabeza del cometa y tiende hacia la parte opuesta al Sol. La primera opinión es de quienes aún no están al tanto de la ciencia de la óptica. Pues el brillo del Sol no se ve en un recinto oscuro, salvo en la medida en que la luz es reflejada por partículas de polvo y humo que siempre están revoloteando por el aire; y por tanto siempre es más luminoso en un medio que contiene humos más densos y estimula mejor al sentido; en un medio más claro (limpio), es más tenue y apenas perceptible; en los cielos, por tanto, sin materia reflectante, no puede darse de ningún modo. La luz no se ve en tanto que está brillando, sino en tanto que desde allí es reflejada hasta nuestros ojos. Pues la visión no ocurre más que por los rayos que inciden en los ojos. Se requiere, pues, alguna materia reflectante en la región de la cola y por esa razón el asunto se torna hacia la opinión tercera. Pues tal materia reflectante no debe encontrarse en otro lugar que en la región de la cola, para que no ocurra que todo el cielo iluminado por la luz solar brille uniformemente. La opinión segunda se presenta con multitud de dificultades. Las colas jamás aparecen adornadas de colores que, por otra parte, suelen ser compañeros inseparables de las refracciones. La luz de las fijas y de los planetas, trasmitida hasta nosotros con distinción, demuestra que el medio celeste no goza de ninguna fuerza refractiva. Pues lo que se dice acerca de que algunas veces fueron vistas por los egipcios estrellas fijas con cabellera, aunque esto acontece muy raramente, debe achacarse a una refracción casual de las nubes. Lo mismo que el parpadeo y centelleo de las fijas han de atribuirse a refracciones bien sea de los ojos, bien del aire en movimiento por cuanto que, al aplicar el telescopio a los ojos, desaparecen. Ocurre por la vibración del aire y de lo vapores ascendentes que los rayos fácilmente sean apartados de vez en cuando del estrecho espacio de la pupila, pero jamás lo son de la más amplia apertura del objetivo de cristal. Y por ello ocurre que se genere el centelleo en el primer caso y cese en el segundo; y el cese en el segundo caso demuestra la transmisión regular de la luz a través de los cielos, sin refracción alguna sensible. Por si acaso alguien pretende que las colas no suelen verse en los cometas, cuando su luz no es bastante fuerte, debido a que entonces los rayos secundarios no tienen bastante fuerza para excitar los ojos y por ello no se ven las colas de las fijas. Ha de saberse que la luz de las fijas puede aumentarse más de cien veces mediante los telescopios y, sin embargo, no se ven colas. La luz de los planetas es también más abundante, y las colas inexistentes; en cambio los cometas tienen frecuentemente muy grande la cola cuando la luz de la cabeza es tenue y muy mortecina. Así el cometa del año 1680, en el mes de Diciembre, momento en el que la luz de su cabeza apenas era igual a las estrellas de segunda magnitud, emitía una cola de notable resplandor de hasta 40, 50, 60 o más grados de longitud; después, el 27 y 28 de Enero, la cabeza parecía una estrella de solo séptima magnitud, mientras la cola, con una luz muy tenue pero bastante perceptible, tenía 6 o 7 grados de largo y, con luz muy oscura que apenas podía verse, se extendía hasta los doce grados o poco más. Pero el 9 de Febrero y el 10, cuando la cabeza dejó de verse a simple vista, observé por el telescopio la cola de dos grados de longitud. Además si la cola se originase de la refracción de la materia celeste y se desviase de la oposición del Sol según la figura del cielo, tal desvío, en las mismas regiones del cielo, debería acontecer siempre en la misma dirección. Ahora bien, el cometa del año 1680, el 28 de Diciembre estaba situado en Piscis 8º 41', visto desde Londres a las 8 p.m., y con una latitud boreal de 28º 6' mientras el Sol se hallaba en Capricornio 18º 26'. Y el cometa del año 1577, el 29 de Diciembre se hallaba en Piscis 8º 41', con latitud boreal de 28º 40', y el Sol estaba también en Capricornio 18º 26' aproximadamente. En ambos casos la Tierra estaba en el mismo sitio y el cometa aparecía en la misma región celeste. Sin embargo, en el primer caso, según observaciones mías y de otros, la cola del cometa se desviaba de la oposición al Sol con un ángulo de 4 grados, hacia el Norte mientras en el último, según observaciones de Tycho, se desviaba hacia el Sur 21 grados; por tanto, descartada la refracción celeste, resta que los fenómenos de las colas se deriven de alguna materia reflectante. Pero unos vapores que sean suficientes para llenar tan vastos espacios y que puedan surgir de las atmósferas de los cometas se explican fácilmente del modo siguiente.

68. El aire y los vapores son de gran rareza en los espacios celestes; y muy pequeña cantidad de vapores basta para producir los fenómenos de las colas

Se sabe que el aire, en la superficie de la Tierra, ocupa 1200 veces más de espacio que el agua de la misma gravedad; y por tanto que una columna cilíndrica de aire de 1200 pies de alto pesa igual que una columna de agua de un pie y de la misma anchura. Pero una columna de aire que llegue hasta lo más alto de la atmósfera iguala con su peso a una columna de agua de aproximadamente 33 pies de alta; y por tanto si de la columna total de aire se retira la parte inferior de 1200 pies, la parte superior restante igualará en peso a una columna de agua de 32 pies. Por ende a la altura de 1200 pies, o de dos estadios, el peso del aire es menor, y por tanto el enrarecimiento del aire comprimido es mayor que en la superficie terrestre en la proporción de 33 a 32. Sabido lo cual es posible ya calcular la rareza del aire en cualquier parte (con la ayuda del Corolario de la Prop. XXII del Lib. II de los Principia) desde la hipótesis de que la expansión del aire es inversamente proporcional a la comprensión: esta proporción está comprobada tanto por los experimentos de Hooke como de otros. Ofrezco los resultados del cálculo en la tabla siguiente, en la cual la primera columna expresa la altura de la atmósfera en millas, de las cuales 4000 equivalen al semidiámetro de la Tierra; la segunda la compresión del aire o el peso; y la tercera la rareza o expansión del mismo aire, supuesto que la gravedad decrezca en razón al cuadrado de las distancias del centro de la Tierra. Se toman aquí los caracteres numerales latinos en lugar de un determinado número de ceros, p. ej., al escribir 0,XVII 1224 en lugar de 0,000000000000000001224 y 26 956 XV en lugar de 26 956 000 000 000 000 000:[12]

TABLA DE AIRE (Altura) (Compresión) (Expansión) 0 33 1 5 17,8515 1,8486 10 9,6717 3,4151 20 2,852 11,571 40 0,2525 136,83 400 0,XVII 1224 26 956 XV 4000 0,CV 4465 73 907 CII 40 000 0,CXCII 1628 20 263 CLXXXIX 400 000 0,CCX 7895 41 798 CCVII 4 000 000 0,CCXII 9878 33 414 CCIX Infinita 0,CCXII 6041 54 622 CCIX

De esta tabla se deduce que el aire al ascender se rarifica, de modo que el aire de alrededor de la Tierra, contenido en la esfera descrita con un diámetro de un codo y después enrarecido en el grado correspondiente a la altura de un semidiámetro terrestre, llenaría todas las regiones planetarias hasta la órbita de Saturno y más; y en el correspondiente a la altura de diez semidiámetros terrestres llenaría más espacios celestes (según el cálculo anterior) que los ocupados por el universo más acá de las estrellas fijas. Y aunque, por la mucho mayor corporeidad de la atmósfera de los cometas y la gran fuerza centrípeta circumsolar, puede ocurrir que el aire no se enrarezca hasta tal punto ni en los espacios celestes ni en las colas de los cometas, no obstante, está claro por este cálculo que una pequeña cantidad de aire y de vapores es suficiente con creces para todos los fenómenos de las colas, puesto que también la gran rarificación de las colas se infiere del hecho de que los astros se vean a través de ellas. La atmósfera terrestre, brillando con la luz del Sol y con el grosor de unas pocas millas, oscurece a todos los astros y casi hasta la propia Luna y los hace prácticamente desaparecer: en cambio, los astros más pequeños se ven a través del enorme grosor de las colas sin la más mínima disminución de claridad.

69. Manera en que las colas pueden originarse de las atmósferas de las cabezas

Kepler adscribe el ascenso de las colas desde las atmósferas de las cabezas y su extensión hacia la parte opuesta al Sol a la acción de los rayos luminosos que arrastran consigo la materia de las colas. Y no está falto de razones el que un aura sumamente tenue en espacios completamente libres ceda a la acción de los rayos, pese a que las sustancias densas, en nuestro mundo muy resistentes, no puedan ser desplazadas sensiblemente por los rayos. Otro autor cree que podrían existir tanto partículas leves como pesadas y que la materia de las colas levita y por su levitación se apartan del Sol. Pero dado que la gravedad de los cuerpos terrestres es como la materia de los cuerpos y por tanto permaneciendo la misma cantidad de materia no puede aumentar ni disminuir, sospecho que tal ascenso procede de la rarificación de la materia de las colas. El ascenso del humo en la chimenea es debido al impulso del aire con el que está mezclado. El aire enrarecido por el calor, asciende debido a la disminución de su gravedad específica y arrastra consigo al humo mezclado. ¿Por qué no ascenderían desde el Sol las colas de los cometas de un modo similar?, pues los rayos del Sol no agitan los medios que atraviesan, salvo por reflexión y refracción. Las partículas reflectantes, calentadas por esa acción, calientan el áurea etérea en que están contenidos. Esta, por el color que le ha sido comunicado, se enrarece y, al disminuir, debido a ese enrarecimiento su gravedad específica por la que antes tendía al Sol asciende a modo de río[13] y arrastra consigo las partículas reflectantes de las que se halla compuesta la cola; ayudando también al ascenso el impulso de la luz solar, como ya se ha dicho.

70. Se muestra que las colas se originan de dichas atmósferas a partir de sus diferentes apariencias

Además se confirma que las colas se originan a partir de las cabezas y ascienden hacia las regiones opuestas al Sol por las leyes que cumplen. Así, porque, estando situados en los planos de las órbitas de los cometas que pasan por el Sol, se desvían de la oposición al Sol siempre en la dirección que deja atrás la cabeza al progresar por dichas órbitas. Porque al espectador situado en dichos planos le aparecen en la región directamente opuesta al Sol, pero, al apartarse de estos planos, poco a poco se observa la desviación y cada vez aparece mayor. Porque la desviación, ceateris paribus, es menor cuando la cola es más oblicua respecto a la órbita del cometa, así como cuando la cabeza se acerca más al Sol. Porque las colas que no se desvían aparecen rectas, mientras que las que se desvían se curvan. Porque la curvatura es mayor, cuando el desvío es mayor y más visible cuando la cola, ceateris paribus, es más larga; pues en las más cortas la curvatura difícilmente es observable. Porque el ángulo de desvío es menor junto a la cabeza del cometa y mayor junto al otro extremo de la cola; y además porque la cola, con su cara convexa mira hacia la región de la que se desvía, la cual está en una línea recta trazada desde el Sol por la cabeza hacia el infinito. Y porque las colas más largas y anchas y que brillan con luz más fuerte sean algo más brillantes por su cara convexa y con bordes menos difusos que por su cara cóncava. Dependen, pues, las apariencias de las colas del movimiento de la cabeza y no de la región celeste en que se ve la cabeza; y por tanto no ocurren por la refracción de los cielos, sino que proceden de la cabeza que desprende materia. Del mismo modo que en nuestra atmósfera el humo de cualquier cuerpo encendido se dirige hacia arriba y esto perpendicularmente si el cuerpo está en reposo, y oblicuamente si el cuerpo se mueve lateralmente, así en los cielos, donde los cuerpos gravitan hacia el Sol, los humos y vapores deben ascender respecto al Sol, como ya se ha dicho, y tender hacia arriba en línea recta si el cuerpo humeante está en reposo, u oblicuamente si el cuerpo en su progreso ha dejado atrás los lugares desde los cuales habían ascendido las partes superiores del vapor. Y esta oblicuidad será menor cuando el ascenso del vapor sea más rápido, a saber en las cercanías del Sol y junto al cuerpo humeante porque allí es más fuerte la fuerza solar aquella por la que el vapor asciende. Por otra parte la columna de vapor se curvará de acuerdo con la diferente oblicuidad y puesto que el vapor del lugar precedente de la columna es un poco más reciente, por ello mismo será aquí un poco más denso y también, por tanto, reflejará más abundantemente y estará delimitado menos imprecisamente, que el vapor del otro lado que irá paulatinamente languideciendo y desapareciendo de la vista.

71. Se prueba por las colas que los cometas a veces descienden por debajo de la órbita de Mercurio

No es cometido, por lo demás, de este lugar dar cuenta de las causas de las cosas naturales. Sean verdaderas o falsas las cosas dichas hasta aquí, al menos esto hemos hallado: que los rayos se propagan desde las colas de los cometas en línea recta por los cielos y por tanto que vienen de los lugares del cielo en que las colas aparecen a los espectadores donde quiera que estos estén situados y además que se expanden desde la cabeza de los cometas hacia las regiones opuestas al Sol y sobre esta base establecemos de nuevo del modo siguiente el límite de las distancias de los cometas.

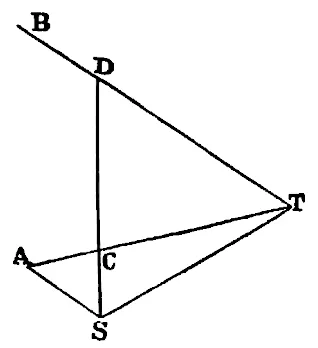
Sean S el Sol; T la Tierra; STA la distancia del cometa hasta el Sol; y ATB la longitud aparente de la cola y, puesto que la luz se propaga desde el extremo de la cola según la recta TB, se hallará dicho extremo en algún punto de la recta TB. Sea D dicho punto, únase DS cortando a TA en C y dado que la cola siempre se opone al Sol aproximadamente y por tanto el Sol, la cabeza del cometa y el extremo de la cola están en línea recta, se hallará la cabeza del cometa en C. Trácese una paralela a TB por SA que concurra con TA en A y la cabeza C del cometa necesariamente se hallará entre T y A, puesto que el extremo de la cola se halla en algún punto sobre la línea infinita TB y todas las líneas SD que pueden trazarse desde S a TB cortan a la línea TA en algún punto entre T y A. Por lo cual el cometa no podría estar más lejos de la Tierra que el intervalo TA, ni del Sol que el intervalo SA más allá de él o ST más acá. Por ejemplo, el 12 de Diciembre de 1680 el cometa estaba a 9 grados del Sol, y la longitud de la cola era de 35 grados como mínimo. Constrúyase pues el triángulo TSA, cuyo ángulo T sea igual a la distancia de 9 grados, y el ángulo A al ángulo ATB o sea a la longitud de la cola de 35 grados y SA será a ST, esto es, el límite de la distancia máxima posible del cometa al Sol al semidiámetro del orbe máximo, como el seno del ángulo T al seno del ángulo A; esto es como 3 a 11 aproximadamente. Por lo cual el cometa en ese momento distaba del Sol de partes de la distancia de la Tierra al Sol; y por tanto discurría o dentro de la órbita de Mercurio o entre dicha órbita y la Tierra. Pero por otra parte, el 21 de Diciembre la distancia del cometa al Sol era de 32 y la longitud de la cola de 70º. Por tanto como el seno de 32 grados al seno de 70 grados esto es como 4 a 7, así era el límite del intervalo entre el cometa y el Sol a la distancia de la Tierra al Sol, y por ende el cometa aún no había rebasado la órbita de Venus. El 28 de Diciembre la distancia del cometa al Sol era de 55 grados y la longitud de la cola de 56 grados. Luego el límite del intervalo entre el cometa y el Sol aún no igualaba la distancia de la Tierra al Sol y por tanto el cometa aún no había rebasado la órbita de la Tierra. De la paralaje se deduce, en cambio, que dicho paso por la órbita terrestre ocurrió el 5 de Enero aproximadamente, y que el cometa descendía mucho por debajo de la órbita de Mercurio. Pongamos que estuvo en el perihelio el 8 de Diciembre, momento de su conjunción con el Sol, y en el recorrido desde el perihelio hasta su salida de la órbita de la Tierra se han consumido 28 días, y por tanto en los 26 o 27 días siguientes en los que dejó de verse a simple vista, apenas si duplicó su distancia al Sol. Con estos mismos argumentos para delimitar las distancias de otros cometas se llega, finalmente, a la siguiente conclusión: Que todos los cometas, mientras son visibles para nosotros, discurren por un espacio esférico con centro en el Sol y radio la distancia del Sol a la Tierra, o el doble o, a lo sumo, el triple.

72. Los cometas se mueven en secciones cónicas que tienen un foco en el centro del Sol y con radios trazados a este centro describen áreas proporcionales a los tiempos

Por lo tanto los cometas, durante todo el tiempo de su aparición, discurren dentro de la esfera de la actividad circumsolar y por tanto se mueven por el impulso del mismo y por ello (por el Cor. I de la Prop. XIII del Lib. I de los Princip). describen secciones cónicas que tienen sus focos en el centro del Sol y con radios trazados al Sol describen áreas proporcionales a los tiempos, pues dicha fuerza, propagándose hacia la inmensidad, rige los movimientos de los cuerpos mucho más allá de la órbita de Saturno.

73. Las secciones cónicas son próximas a parábolas. Esto se sigue de la velocidad de los cometas

Por lo demás tres son las hipótesis sobre los cometas: o bien que se originan y se destruyen cuando aparecen y desaparecen, o bien que proviniendo de la región de las fijas atraviesan nuestro sistema planetario, o bien, finalmente, que giran perpetuamente en torno al Sol en órbitas muy excéntricas. En el primer caso los cometas se moverían en secciones cónicas de cualquier clase de acuerdo con sus diferentes velocidades; en el segundo se moverán en hipérbolas; en uno y otro frecuentarían indistintamente todas las regiones tanto las polares como las de la Eclíptica; en el tercer caso los movimientos ocurrirían en elipses muy excéntricas y muy cercanas a la forma de parábolas; pero las órbitas, si ha de preservarse la ley de los planetas, no se desviarán mucho del plano de la Eclíptica. Y por cuanto he podido observar hasta aquí, es lo tercero lo que ocurre. Porque los cometas frecuentan en gran medida el zodiaco y casi nunca alcanzan una latitud heliocéntrica de cuarenta grados. Se mueven también en órbitas muy próximas a parábolas como deduzco de sus velocidades. Pues la velocidad con que se describirá una parábola es siempre a la velocidad con la que un cometa o planeta puede girar en torno al Sol en círculo a la misma distancia como la raíz cuadrada de 2 a 1 (por el Cor. 7 de la Prop. XVI). Y según mi cálculo semejante velocidad ha sido establecida para los cometas. He examinado el asunto deduciendo sucesivamente las velocidades a partir de las distancias, y las distancias a partir de las paralajes y de los fenómenos de las colas conjuntamente. Los errores en las velocidades, por exceso o por defecto, no resultaron mayores que los que hubieran podido producirse desde los errores en las distancias obtenidas según aquella razón. Pero yo he utilizado un argumento del estilo siguiente.

74. En cuánto tiempo los cometas en trayectorias parabólicas recorren el Orbe Máximo

Dividido el radio del Orbe máximo (órbita de la Tierra) en 1000 partes, representan los números de la primera columna de la tabla siguiente la distancia del vértice de la parábola al centro del Sol expresada en tales partes; y el cometa, en los tiempos expresados en la segunda columna, se moverá desde el perihelio hasta la superficie de la esfera que se describe con centro en el Sol y radio del Orbe Máximo; y en los tiempos expuestos en las columnas 3, 4 y 5 duplicará, triplicará o cuadruplicará esa su misma distancia al Sol.

Tiempo en que los comentas entran dentro del Orbe Máximo y salen de él. El momento en el cual los cometas entran dentro de la esfera del Orbe Máximo y salen de él se infiere de la paralaje; pero de modo más rápido por la tabla II.

75. Con qué velocidad los cometas de 1680 atravesaron el Orbe Máximo

El ingreso o la salida ocurre en el tiempo de las distancias del cometa al Sol expresadas en la columna primera del sector de los movimientos diurnos. Así el 4 de Enero de 1681 (sistema antiguo) el movimiento aparente diurno del cometa en su órbita era casi de 3 grados 5 minutos. La distancia correspondiente a este era de 71 grados y el cometa alcanzó esta distancia del Sol el día 4 hacia las 6 de la tarde. Por otra parte el 11 de Noviembre de 1680 el movimiento diurno del cometa que entonces apareció era de casi 4 grados y la distancia correspondiente a él de 79 grados se alcanzó el 10 de Noviembre un poco antes de media noche. Pues bien, en estos períodos de tiempo los cometas han alcanzado una distancia como la que tenía la Tierra al Sol, mientras la Tierra estaba entonces prácticamente en el perihelio. La tabla primera se ha computado con la distancia media de la Tierra al Sol tomada como 1000 partes, y esta distancia es mayor que el intervalo que puede recorrer la Tierra en casi un día de su movimiento anual o el cometa con su movimiento en 16 horas. Para reducir el cometa a esta distancia media de 1000 partes, añádanse al tiempo anterior y sustráiganse del posterior 16 horas y el tiempo primero resultará ser el 4 de Enero a las diez de la tarde y el segundo el 10 de Noviembre sobre las 6 de la mañana. Del tenor y progreso de los movimientos diurnos se sigue que la conjunción de ambos cometas con el Sol estuvo entre el 7 y el 9 de Diciembre, y por tanto de esta fecha hasta el 4 de Enero a las 10 de la tarde por una parte y hasta el 10 de Noviembre a las 6 de la mañana por otra, hay aproximadamente 28 días. Y todos estos días (por la Tabla I) debían consumirse en trayectorias parabólicas.

76. Estos cometas no fueron dos, sino uno y el mismo cometa. Se explica más exactamente con qué órbita y con qué velocidad cruzó el cielo

Por lo demás, de la coincidencia de perihelios y de la coincidencia de velocidades es verosímil que estos dos cometas, que hemos considerado antes como dos, no fuesen dos sino uno y el mismo cometa. Por aquella razón la órbita de este cometa sería o una parábola o una sección cónica no muy distinta de una parábola y casi tangente a la superficie del Sol en el vértice. Pues, por la Tabla II, la distancia del cometa a la Tierra era el 10 de Noviembre de 360 partes aproximadamente y de 360 el 4 de Enero. De ello y de las longitudes y latitudes del cometa se sigue que las distancias entre los lugares en que entonces se hallaba respectivamente era como de 280. La mitad de esto, o sea 140, es la ordenada a la órbita del cometa que corta una parte de su eje casi igual al radio del Orbe Máximo, esto es de 1000 partes. Y de aquí, dividiendo el cuadrado de la ordenada, esto es de 140 por 1000, parte abscisa del eje, se obtiene el lado recto de 19,6, en números redondos 20, cuya cuarta parte, 5, es la distancia entre el vértice de la órbita y el centro del Sol. A la distancia de 5 partes en la Tabla primera le corresponden 27 días 16 horas 7 minutos. En dicho tiempo el cometa completará su recorrido en la órbita parabólica entre su perihelio y la superficie esférica del Orbe Máximo descrito con un radio de 1000 partes, y por tanto el doble de dicho tiempo, o sea 55 días y 1 horas, consumirá en todo su movimiento dentro de la Órbita Mayor. Y esto es lo que ocurre. Pues desde el 10 de Noviembre a las 6 de la mañana cuando el cometa entró en esta órbita hasta el 4 de Enero a las 10 de la tarde cuando salió de ella hay 55 días y 15 horas. La diferencia de 7 horas en este cálculo rudimentario debe despreciarse y quizá pudiera proceder de un movimiento un poco más lento realizado en la órbita elíptica. Entre el ingreso y la salida el tiempo medio se sitúa en 8 de Diciembre a las 2 de la mañana. Por tanto en este momento debió hallarse el cometa en el perihelio. Y he aquí que Halley este mismo día, un poco antes de la salida del Sol, vio una cola corta, ancha y muy brillante, como hemos dicho, que surgía perpendicularmente del horizonte. De la situación de la cola se infiere que el cometa ya había rebasado la Eclíptica y tenía una latitud boreal; y por tanto el perihelio que estaba en la otra parte de la Eclíptica, ya había sido entonces rebasado, aunque aún no hubiese alcanzado el meridiano del Sol. Y así, al estar entre el perihelio y la conjunción solar, el cometa estaba unas pocas horas antes en el perihelio, pues en semejante cercanía del Sol debió moverse a gran velocidad y recorrer casi medio grado aparente por cada hora.

77. Se muestra con muchos ejemplos con qué velocidad se mueven los cometas

Mediante cálculos semejantes deduzco que el cometa de 1618 entró en el límite esférico del Orbe máximo el 7 de Diciembre a la puesta del Sol. Ocurrió pues su conjunción con el Sol en torno al 9 o 10 de Noviembre; median casi 28 días, como en el cometa anterior, pues del tamaño de la cola, que fue similar a la del cometa anteriormente descrito, es muy posible que este, de igual modo, casi llegase a rozar el cuerpo del Sol. Brillaron este año cuatro cometas, de los cuales este fue el último; el segundo, que primeramente fue visto en las proximidades del Sol naciente el 31 de Octubre y después se desvaneció enseguida bajo los rayos del Sol, sospecho que fue el mismo que el cuarto, el cual emergió de entre los rayos del Sol hacia el 9 de Noviembre. Añádase a esto que el cometa de 1607 entró en la esfera del Orbe Máximo el 14 de Septiembre del calendario antiguo y alcanzó su mínima distancia al Sol sobre el 19 de Octubres median 35 días. Esa distancia del perihelio al Sol subtendía un ángulo aparente a la Tierra de aproximadamente 23 grados, y por tanto era de 390 partes: pero en la Tabla I tales partes responden a 34 días aproximadamente. Además, el cometa de 1665 entraba en la esfera de la órbita anual hacia el 17 de Marzo y alcanzaba el perihelio hacia el 16 de Abril, mediando 30 días. La distancia entre el perihelio y el Sol subtendía en la Tierra un ángulo de casi 7 grados y por tanto era de casi 122 partes: y a estas partes en la Tabla I les corresponden 30 días. Por otra parte, el cometa del año 1682 entraba en la esfera del Orbe Máximo hacia el 11 de Agosto y llegaba al perihelio hacia el 16 de Septiembre distando entonces del Sol un intervalo de unas 350 partes a las que corresponden, en la Tabla I, 33 días. Por fin, aquel célebre cometa de Regiomontano que en 1472 pasa por la región del polo norte y completa en un solo día una trayectoria de cuarenta grados, y viene a entrar en el límite del Orbe Máximo el 21 de Enero, momento en que pasaba por el polo; y desde allí dirigiéndose hacia el Sol se ocultaba bajo los rayos solares en los últimos días de Febrero. De donde es verosímil que se consumiesen treinta días o pocos más entre dicho ingreso y el perihelio del cometa, puesto que en realidad este cometa no sería más rápido que los demás cometas, ni tampoco por otra razón habría alcanzado tamaña velocidad aparente que por su paso por las cercanías de la Tierra.

78. Se propone determinar la órbita de los cometas

La velocidad de los cometas, por tanto, es, en la medida en que pueda ser determinada mediante estos cálculos un tanto rudimentarios, la misma que aquella con la que las parábolas, o las elipses afines a ellas, puedan ser descritas: y por lo mismo, de la distancia dada entre el cometa y el Sol, se obtiene muy aproximadamente y de aquí surge el problema siguiente:

PROBLEMA

Se da la relación entre la velocidad del cometa y su distancia al centro del Sol; hállese la trayectoria.

Una vez resuelto este problema se tendrá por fin un método para determinar exactamente las trayectorias de los cometas. Pues si dicha relación se asume dos veces y se calcula a partir de aquí otras dos y después mediante la observación se establece el error de una y otra trayectoria, puede corregirse la asunción mediante la regla de la falsa posición y hallar así una tercera trayectoria que coincida plenamente con la observación. Y determinando por este método las trayectorias de los cometas se puede saber por fin con exactitud qué regiones vienen a recorrer estos cuerpos, cuánta sea su velocidad, de qué tipo sean sus trayectorias y cuáles sean las magnitudes reales de las colas, lo mismo que las formas según las distintas distancias de las cabezas respecto al Sol. Incluso es dado esperar que por este método pueda saberse por fin si los cometas completan la órbita en tiempos dados y en qué períodos de tiempo se completan las revoluciones de cada uno. Se resuelve pues el problema, estableciendo primero mediante tres o más observaciones el movimiento horario de los cometas en un tiempo dado y derivando después a partir de este movimiento la trayectoria. De este modo la trayectoria depende de una sola observación y del movimiento horario en el tiempo de dicha observación; y por tanto o bien se confirma a sí misma o se disconfirma; pues la conclusión que se deduce del movimiento de una hora y de otra y de una hipótesis falsa, jamás se ajustará a los movimientos del cometa de principio a fin. El método de cálculo en su totalidad es como sigue:

EN LA SOLUCIÓN DEL PROBLEMA SE ANTEPONEN UNOS LEMAS.

Lema I

Dadas en posición dos rectas OR, TP, cortarlas con una tercera RP formando el ángulo recto TRP, de tal modo que si la recta SP se traza hasta un punto dudo S, venga dado al sólido contenido por dicha recta SP y el cuadrado de la recta OR terminada en un punto dudo O.

Gráficamente se hace así: sea dicho contenido dado M2 × N. Sobre un punto cualquiera r de la recta OR eleva una perpendicular rp que toque a TP en p. Y por los puntos S, p traza Sq igual a . De igual modo traza tres o más rectas, S2q, S3q, etc., y trazada una línea regular por todos los puntos q, 2q, 3q, cortará a la recta TP en el punto P desde el que hay que elevar la perpendicular PR.

Trigonométricamente así: Tómese la línea últimamente hallada TP, y desde aquí en los triángulos TPR, TPS se tendrán dadas las perpendiculares TR, SB, y en el triángulo SBP el lado SP y el error . Haz que este error, llámese D, sea a un nuevo error, llamémosle E, como el error 2p2q ± 3p3q al error 2p3p, o como el error 2p2q ± D al error 2pP; y el nuevo error sumado o restado a la longitud TP dará la longitud correcta TP ± E. La elección de la suma o la resta se discierne de la observación del esquema. Si por casualidad fuese necesaria una ulterior corrección, repítase la operación. Aritméticamente así: Supongamos el esquema hecho, y sea la línea TP hallada gráficamente de longitud correcta TP + e; y las longitudes correctas de las OR, BP y SP serán:

De donde por el método de series convergentes será:

En lugar de los términos dados

escríbase:

y teniendo en cuenta los signos tendremos

De aquí, despreciando el término muy pequeño resulta e = -G. Si el error no fuese despreciable tómese

Y adviértase que se insinúa este método general de resolver los problemas más difíciles tanto trigonométricamente como aritméticamente sin los enrevesados cálculos y resoluciones de ecuaciones artificiosas que hasta ahora estaban en uso.

Lema II

Dadas tres rectas en posición, cortarlas con una cuarta cuyas partes entre cortes tengan una proporción mutua dada y que pase por un punto dado en una de aquellas.

Sean las rectas en posición dada AB, AC, BC, y sobre AC desde el punto D. Trácese la recta DG paralela a AB que toca a BC en G. Tómese GF a BG según aquella proporción dada y trácese FDE; y FD será a DE como FG a BG.

Trigonométricamente así: En el triángulo CGD se dan los ángulos y el lado CD y de aquí los demás lados, y por estar dadas las razones vienen dadas también las líneas GF y BE.

Lema III

Hallar y representar gráficamente el movimiento horario de un cometa en un tiempo dudo.

Dense tres longitudes del cometa según observaciones dignas de crédito. Sean sus diferencias ATR, RTB y trátese de hallar el movimiento horario en el tiempo de la observación intermedia TR. Trácese (por el Lema II) la recta ARB, cuyas partes cortadas AR, RB, son como los tiempos entre las observaciones. Y si el cuerpo en todo el tiempo recorre toda la línea AB uniformemente y es mientras tanto observado desde T, este será su movimiento aparente en el punto R que es el mismo del cometa aproximadamente en el momento de la observación TR.

Lo mismo más exactamente.

Dense las longitudes más distantes a uno y otro lado Ta y Tb, y (por el Lema II) trácese aRb cuyas partes aR, Rb son como los tiempos entre las observaciones aTR, RTb. Corte esta a las líneas TA, TB en D y E; y puesto que el error de la inclinación TRa crece casi en razón del cuadrado del tiempo entre observaciones, traza FRG, de tal modo que, o bien el ángulo DRF respecto al ángulo ARF, o bien la línea DF respecto a la línea AF, sean como el cuadrado de la razón entre el tiempo total entre las observaciones aTb y el tiempo total entre las observaciones ATB, y en lugar de la línea hallada antes AB, tómese ahora la línea recién hallada FG.

Es conveniente que los ángulos ATR, RTB, aTA, BTb no resulten menores de diez o quince grados y los tiempos que les corresponden no mayores de ocho o doce días, y tomar las longitudes cuando el cometa se mueve a mayor velocidad. De este modo los errores de observación tendrán una proporción menor respecto a las diferencias de longitudes.

Lema IV

Hallar las longitudes de un cometa en tiempos dados.

Se hace tomando sobre la línea FG, las distancias Rr, Rh proporcionales a los tiempos y trazando las líneas Tr, Th. La operación trigonométrica es clara.

Lema V

Hallar las latitudes.

Sobre los radios TF, TR, TG, elévense las normales Ff, RP, Gg, tangentes de las latitudes observadas. Trácese PH, paralela a la recta fg. Las perpendiculares sobre PH, tales como rp, hH, serán las tangentes de las latitudes buscadas a los radios Tr, Th.

PROBLEMA I

Determinar la trayectoria de un cometa desde una razón asumida de velocidad.

Sea S el Sol; t, T, q, tres lugares equidistantes de la Tierra en su órbita; p, P, h, los lugares respectivos correspondientes de un cometa en su trayectoria interpuestos entre cada uno de ellos intervalos de una hora; pr, PR, ho, sean perpendiculares trazadas al plano de la Eclíptica, y rRo la proyección de la trayectoria en dicho plano. Únanse Sp, SP, Sr, SR, ST, tr, TR, qo, TP y coincidan tr y qo en O: también TR convergerá en O muy aproximadamente, o el error será despreciable. Por los Lemas precedentes están dados los ángulos r O R, R O q, así como las razones pr a tr, PR a TR,, ho a qo. También está dada la figura tTqO en magnitud y en posición a la vez que la distancia TS y los ángulos sTr, PTR, STP. Supongamos que la velocidad del cometa en el punto p es a la velocidad del planeta que gire en círculo a la misma distancia SP del Sol como v a 1; y tendremos que determinar una línea pPh con esta condición: que el espacio ph descrito por el cometa en dos horas sea el espacio V × tq, esto es al espacio que la Tierra describe en el mismo tiempo multiplicado por el número V, como la raíz cuadrada de la razón de la distancia de la Tierra al Sol ST a la distancia SP del cometa al Sol; y que el espacio pP, descrito por el cometa en la primera hora, sea al espacio Ph, descrito por el cometa en la segunda, como la velocidad en p a la velocidad en P; esto es, como la raíz cuadrada de la razón entre la distancia SP y la distancia sP, o sea en razón 2SP a SP + sp. Estoy despreciando en toda esta operación pequeños restos que no llegan a crear error perceptible.

En primer lugar, por tanto, al igual que los matemáticos en la resolución de ecuaciones artificiosas como primer paso infieren una raíz por conjetura, del mismo modo en esta operación analítica, haciendo una conjetura establezco en cuanto puedo la distancia buscada TR y (por el Lema II) trazo ro, primero de modo tal que rR y Ro sean iguales; y después (una vez hallada la razón entre SP y Sp dimanante de aquí) de modo que rR sea a Ro como 2SP a Sp + SP; y hallo las razones de las líneas Ph, ro, y OR entre sí. Supóngase que M es a v × tq como OR a Ph y por las proporcionalidades: (Ph)2: (v × tq)2 :: ST : SP, tendremos inmediatamente que (OR)2 : M2 :: ST : SP y por tanto el sólido contenido en (OR)2 × SP igual al dado en M2 × ST. De donde, si los triángulos STP, PTR se colocan ahora en el mismo plano, vendrán dadas TR, TP, SP, PR (por el Lema I). Todo esto lo realizo primero gráficamente, rápida y toscamente; después, gráficamente, pero con mayor cuidado; finalmente por cálculo numérico. Entonces, de nuevo, determino el lugar de las líneas ro y Ph del modo más exacto junto con los nodos y la inclinación del plano SPh respecto al plano de la Eclíptica; y en tal plano SPh (por la Prop. XVI del Lib. I de los Princip. Mat.), describo la trayectoria en que se moverá el cuerpo lanzado desde un punto dado P según la recta dada Ph, con tal velocidad que sea a la velocidad de la Tierra como Ph a V × tq.

PROBLEMA II

Corregir la razón asumida de velocidad y la trayectoria hallada.

Tómese la observación del cometa hacia el final del movimiento, o alguna otra lo más distante posible de las observaciones tomadas anteriormente; y búsquese la intersección del radio trazado al cometa en aquella observación con el plano SPh, así como el lugar del cometa en la trayectoria al tiempo de aquella observación. Si dicha intersección coincide con este lugar es prueba de que la trayectoria fue hallada correctamente. Si no coincide, habrá de tomarse un nuevo número V y hallarse una nueva trayectoria; después habrá que establecer el lugar del cometa en esta trayectoria al tiempo de la observación probatoria susodicha y determinar la intersección del radio con el plano de la trayectoria como antes. Y de la comparación de la variación del error con la variación de otras cantidades se inferirá mediante la Regla Áurea, qué cantidades deberán variar o corregirse en aquellas otras cantidades para que el error resulte lo más pequeño posible. Hechas estas correcciones se tendrá la trayectoria con bastante exactitud, supuesto que las observaciones que basaron el cálculo fueron exactas y que no se erró mucho al asumir la cantidad V, pues si se erró mucho deberá repetirse la operación hasta que se encuentre la trayectoria con suficiente exactitud.