Introducción

Nació Sir Isaac Newton el veinticinco de diciembre de 1642 en la granja de Woolsthorpe, Lincolnshire, y murió en Londres-Kesington el veinte de marzo de 1727 tras ochenta y cuatro años, tres meses y veintitrés días de vida llenos de éxitos intelectuales por una parte y de felicidad y tranquilidad por otra.

Su padre murió muy poco antes de nacer Sir Isaac y era un más que mediano granjero, dueño de la hacienda de Wollsthorpe, propiedad de la familia desde hacía generaciones. Ante el hecho prematuro de su muerte se pensó en que Sir Isaac, llegado el tiempo, continuase con la explotación de la granja paterna. Mas, entre tanto, su madre se casó de nuevo con el reverendo Bernabé Smith, un clérigo bien acomodado, y se fue a vivir con su esposo al cercano pueblo de North Witham. Sir Isaac quedó en Woolsthorpe al cuidado de sus abuelos. Pero, al quedar viuda de nuevo, su madre regresó a la granja de los Newton con los tres hijos habidos del segundo matrimonio. Newton tenía para entonces catorce años.

Durante la primera infancia había asistido a dos pequeñas escuelas para externos y desde los doce asistió a la King’s School de Gratham viviendo durante este tiempo como pupilo en casa de un boticario. Ya entonces daba la impresión de ser un muchacho «tranquilo, silencioso y reflexivo» pero lleno de imaginación. Se divertía construyendo artilugios con los que provocaba admiración entre sus compañeros y así se habla de un molino de viento, una clepsidra o reloj de agua, un carricoche que hacía andar con una manivela el ocupante que subía a bordo, cometas que volaban más alto y se manejaban mediante articulaciones y, a veces, les colocaba luces en su interior que asustaban a los buenos campesinos o al menos les hacía creer que se trataba de auténticos meteoros, y por supuesto construía relojes de sol para lo que se dedicaba a observar y trazar sobre el patio de la casa donde vivía el curso diurno del astro solar, etc.

Pero la llegada a Woolsthorpe de su madre vino a alterar estas alegres diversiones y tuvo que regresar a la granja para, como hijo mayor, hacerse cargo de su dirección. Sin embargo no tenía el menor interés en aquellas cosas y cuando menos se esperaba se le hallaba absorto leyendo bajo un seto mientras los animales a su cuidado campaban libremente por los campos, de modo que su madre, aconsejada por el antiguo profesor de Gratham y por el tío de Newton, se decidió a que continuase sus estudios y después ingresase en la Universidad. Así ocurrió que regresó a Gratham y después ingresó en el Trinity College de Cambridge el cinco de junio de 1661 a los dieciocho años como becario. Eran los días en que se acababa de producir la restauración de los Estuardo (1660) en la persona de Carlos II y los profesores de Cambridge cambiaban la gorra redonda del anterior régimen por el cuadrado birrete resolviendo así, de paso, el problema matemático tan debatido de la «cuadratura del círculo» según comentario irónico de un matemático de la época.

Llevó por este tiempo un diario de sus estudios y por él conocemos con cierto detalle cómo se desarrollaron. No había estudiado matemáticas anteriormente, aunque estaba familiarizado con la lógica a través de un texto de Sanderson que era una especie de introducción obligada a los estudios matemáticos. Leyó después a Euclides y no encontró dificultad alguna en comprender la obviedad de sus enunciados. Después trabajó un libro de texto titulado Clavis malhematicae de William Oughtred que se había publicado en 1631 así como la Geometría de Descartes que le causa una magnífica impresión pese a ciertas dificultades para su lectura. Continuó luego con la Optica de Kepler, la obra de Vieta y la Arithmetica infinitorum de Wallis a la vez que seguía las lecciones de Barrow.

El año 1665 se declaró una terrible peste en Londres que se fue extendiendo y en el otoño alcanzó a las ciudades universitarias obligando con ello a cerrar las universidades de Cambridge y Oxford. Por esto Newton se vio en la necesidad de retirarse a su granja durante el otoño de 1665 y el año 1666, recién graduado como bachiller de Artes. Durante ese período permanece en su casa y realiza estudios que en cierto modo van a ser decisivos por cuanto en ellos se halla la base y el núcleo de lo que va a constituir su gran aportación científica.

En primer lugar formuló, al menos de un modo provisional, el principio fundamental de su teoría de la gravitación, esto es, que cada partícula de materia atrae a otra partícula y ello en proporción directa al producto de sus masas y en proporción inversa al cuadrado de sus distancias. No obstante el fundamento para esta hipótesis, no parece que llegase Newton a establecerlo hasta más tarde y por el momento solo debió parecerle una buena hipótesis de trabajo e incluso una mera parte del conjunto de principios que habrían de gobernar la concepción mecánica del mundo.

En segundo lugar dejó redactado un esbozo más que medianamente completo del cálculo de fluxiones. Así, en un manuscrito de 28 de mayo de 1665 ya hay pruebas de que está utilizando las fluxiones para sus cálculos así como de que por estos mismos días —son los días de su bachillerato en Artes— ha formulado ya su teorema del binomio. En otro manuscrito de 13 de noviembre de 1665 utiliza las fluxiones para hallar la tangente y el radio de una curva en un punto de la misma. De todo eso dará cuenta a sus amigos y alumnos hacia 1669 al ser nombrado profesor

Además, y este es tercer núcleo de sus trabajos en esta época, trabajó en pulir lentes no esféricas —siguiendo aquí la opinión de Descartes— iniciando los estudios sobre la luz blanca del Sol y logrando tal vez descomponerla en colores.

A la sazón su planteamiento de la teoría de la gravedad era más o menos así: Si se supone que la fuerza que retiene a la Luna en su órbita es la misma que actúa en forma de gravedad sobre una piedra que cae en las inmediaciones de la Tierra y se sabe que la velocidad de caída de esta es de 16 pies en el primer segundo, entonces se podría formular el problema para la Luna del modo siguiente:

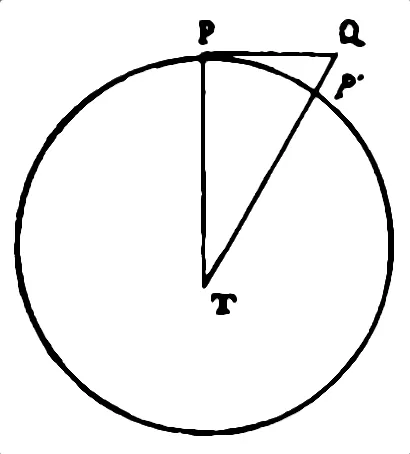
La órbita de la Luna en torno a la Tierra es aproximadamente un círculo. La distancia de la Luna a la Tierra es conocida aproximadamente y, por tanto, la longitud de su órbita. También es conocido el tiempo que tarda en dar una vuelta completa en torno a la Tierra. De aquí que pueda determinarse la velocidad de la Luna en el momento y punto P. En el segundo siguiente la Luna debería hallarse en el punto Q si no fuese atraída hacia T por la fuerza de la gravedad. Pero al cabo de ese segundo la Luna no se halla en Q sino en P’ y por tanto la Tierra ha «tirado» de la Luna haciéndola recorrer la distancia QP’ en un segundo. Suponiendo que la gravedad sea una fuerza constante y que solo ella actúe en el caso y lo hiciese según la ley del inverso del cuadrado de las distancias, entonces QP’ debería ser a 16 pies inversamente como el cuadrado de la distancia de la Luna al centro de la Tierra es al cuadrado del radio de la Tierra.

Y aunque este planteamiento es básicamente correcto, los datos de estas distancias de que entonces disponía Newton lo llevaron a un resultado en el que QP’ era un octavo menor de lo que debía ser. Solo en 1679, como veremos, al repetir los cálculos sobre datos más exactos halló que QP’ se ajustaba al valor referido.

En 1667 regresó a Cambridge y, ya Maestro en Artes, fue elegido como miembro del Trinity College donde fijó su residencia y desde octubre de 1669 fue profesor Lucasiano de matemáticas hasta su renuncia en 1701. Como titular de esa cátedra pronunció las famosas «Lectures» en las que expone casi todo el material de sus descubrimientos científicos. Curiosamente, sin embargo, estas «Lectures» no fueron muchas veces nada concurridas y en ocasiones regresaba a casa desde una sala vacía.

Todas ellas tratan de los temas que hemos mencionado más arriba: desde 1669-70 a 1672-73 el tema es la óptica; desde 1673-74 a 1683-84 son temas matemáticos y desde 1684 a 1687 los temas son mecánicos y astronómicos, «de motu corporum». Habría que observar que todos estos temas de las «Lectures» newtonianas fueron objeto de su consideración con anterioridad a serlo de su pública exposición y obedecen por tanto a investigaciones previas en las que Newton ha llegado a determinados resultados que son el objeto de su exposición pública. Así ocurre que desde finales de 1669 elige como tema para sus lecciones los resultados de sus experimentos ópticos y va exponiendo sus hallazgos sobre la descomposición de la luz blanca en colores mediante un prisma y la consiguiente explicación del arco iris. De ello da cuenta a la Royal Society en una comunicación de 19 de febrero de 1671-72, publicada en el número 80 de las Philosophical Transactions. Pero un fracaso en sus experimentos encaminados a corregir la aberración cromática de dos colores mediante un juego de prismas le decidió a abandonar la idea de hacer un telescopio de refracción que fuera acromático y en su lugar diseñó uno de reflexión del que da cuenta otro escrito de marzo de 1672. Ambas cosas le acarrearon una larga correspondencia que lo cantaba, cuando no lo irritaba, por el mero hecho de que alguien se atreviera a discutir sus bien establecidas conclusiones. Así lo manifiesta en carta de 9 de diciembre de 1675 de la que Fontenelle se hace eco en su Elogio.

Por estos años Newton desarrolla su trabajo matemático, que va exponiendo en sus «Lectures», principalmente de álgebra, teoría de ecuaciones y algunas cuestiones geométricas en relación con el análisis de curvas así como el método de fluxiones. También en este caso debe tenerte en cuenta la alta cuota de participación que debe atribuirse a los temas y descubrimientos de 1655-66. No obstante, el corpus de tantad «Lectures» abarca cuestiones algebraicas notablemente desarrolladas a partir de aquellos planteamientos iniciales. Cuando en 1707 Whinston publicó el Algebra universalis conteniendo la parte más significativa de las «Lectures» había ya un cierto conocimiento de los hallazgos matemáticos de Newton, parte por los apéndices de la Optica, publicados en 1704, y parte porque entre los medios matemáticos había circulado material manuscrito procedente de sus discípulos de Cambridge o a veces de sus amigos, como Collins, cuando no inferido de algunos lemas y problemas de los Principia en los que había hecho uso restringido de esos análisis, si bien no publicase más que los resultados de los mismos. Pero, esto no obstante, la obra matemática de Newton en su conjunto no se acabó de publicar hasta bien andado el siglo XVII y en concreto la Geometría Analítica no apareció hasta que Sir Samuel Horsley la incluyó en el tomo I de las Opera en 1779. En este capítulo entra de lleno la célebre polémica con Leibniz sobre el descubrimiento del cálculo infinitesimal (las fluxiones). Parece que Leibniz llegó a formularlo consistentemente hacia 1676-78 y publicó su método en las Acta Eruditorum en 1682. Suscitada la cuestión de su paternidad. Newton la reclamó desde su preponderante presidencia de la Royal Society y obligó a esta a intervenir con un dictamen que, en honor a la verdad, tampoco satisfizo por completo a Sir Isaac puesto que solo dejó establecido que Newton conocía este método desde 1669 o antes, pero que de ningún modo podía demostrarse que Leibniz lo hubiese tomado de Newton directa o indirectamente —plagio— o que Leibniz no lo hubiese hallado por sí mismo. Newton dedicó a esta cuestión mucho de su tiempo desde 1709 a 1716, pero también es verdad que ya para esta época había abandonado la investigación y —aparte sus obligaciones en el Mint— cuidaba solo de estas cosas y de la segunda edición de los Principia que estaba encomendada a Roger Cotes.

En el año 1779 conoce Newton, posiblemente por una carta de Hooke, las mediciones geodésicas de Picard. En ellas Picard utiliza un valor del radio de la Tierra prácticamente correcto y Newton, sobre la base de los datos de Picard, repite sus cálculos de 1666 relativos a la órbita lunar y halla que los resultados concuerdan con las exigencias de su hipótesis de la gravitación bajo la estipulación de la ley del inverso del cuadrado. A continuación generaliza la teoría para toda partícula que bajo la acción de una fuerza centrípeta gire en torno a un punto y demuestra que el radio trazado entre la partícula y su centro de giro barrerá áreas iguales en tiempos iguales. Esto era la, hasta ahora empírica, ley de Kepler de las áreas. También halla que si una partícula describe una elipse bajo la acción de una fuerza centrípeta, situada esta en un foco, dicha fuerza deberá ajustarse a la ley del inverso del cuadrado y, viceversa, que la órbita de una partícula que gire bajo la acción de una fuerza centrípeta de estas características tiene que ser una cónica y más exactamente una elipse. Pero Newton, una vez más, no publica sus descubrimientos, quizás porque no tiene el menor deseo de iniciar otra larga correspondencia con sus oponentes que según podía intuir habrían de ser muchos, sobre todo cartesianos, de cuyo modo de hacer filosofía natural aborrecía con vehemencia.

Pero en este caso fue cierto eso de que «el buen paño en el arca se vende» y en agosto de 1684 Halley se presentó en Cambridge para consultar a Newton sobre la ley de Kepler según la cual el tiempo periódico de un planeta varía como el cubo del radio de su órbita. Parece que Hooke, Halley, Huygens y Wren habían supuesto la ley del inverso del cuadrado pero no podían deducir a partir de ella la órbita que bajo esas condiciones debería describir un planeta. Newton contestó en el acto que ya lo había calculado y era una elipse. Y al no encontrar sus papeles a mano para mostrárselos a Halley, le prometió una copia en limpio con la demostración que había establecido en 1679. Con ese estímulo Newton, en ese otoño de 1684, redactó las proposiciones 1 a 19, 21, 30, 32 a 35 del libro I de los Principia, cosa que, con algunos comentarios más, vino a constituir el tema de «Lectures» de ese otoño. En noviembre recibió Halley el manuscrito prometido por Newton y esto le movió a volver a visitarlo. De esa visita debió salir el proyecto general de los Principia al menos en la mente de Newton. Esta obra consta, como es sabido, de tras libros. Lo dos primeros establecen las bases físico-matemáticas de un sistema general de mecánica, sistema que es aplicado en el tercero a los movimientos planetarios del sistema solar como un caso particular del sistema general de mecánica establecido en los dos primeros. En estos la teoría considera a los cuerpos como puntos, y no como cuerpos extensos. En el tercero, los cuerpos celestes son asimilados a esos puntos mediante la sustitución del cuerpo por su centro, sobre el que se acumula toda la masa, todo el peso y toda la gravedad del mismo. El esfuerzo de Newton en este tiempo es titánico y el 28 de abril de 1686 hace entrega del libro primero a la Royal Society. En el verano de 1686 completa el libro segundo y en septiembre de ese año ya está preparando el libro tercero que llevará por subtítulo «De mundi systemate liber». En todo este trabajo ocupó el invierno y la primavera de modo que en el verano de 1687 y con la inapreciable ayuda de Halley, que fue en cierto modo, hasta económico, su editor, apareció la primera edición de la obra más importante y más influyente de Newton: Philosophiae Naturalis Principia Mathematica.

En su composición utilizó un método matemático-geométrico que hoy no se utiliza al haber sido sustituido por el cálculo. El mismo Newton utilizaba para obtener sus resultados sus métodos de fluxiones, aunque después hiciese sus demostraciones y la presentación de las mismas en lenguaje geométrico. Por ello resulta, y quizá ya lo era un poco en tu tiempo, arcaizante. Pero, por otra parte, Newton sabía que los secretos del cálculo por entonces solo los poseía el mismo y, para el común de los matemáticos y científicos, ese lenguaje geométrico era todavía el lenguaje usual. Por tanto quizá pensó que, si le comprendían mejor, le ahorrarían explicaciones y le evitarían molestias.

El libro que aquí presentamos está profundamente relacionado con la composición de los Principia. Para dar cuenta de lo que Newton expone en el tratado que el lector tiene en tus manos juzgó Newton necesario componer una obra de tal envergadura y cuando la hubo compuesto juzgó conveniente suprimir de ella este tratado y colocar en su lugar el libro tercero que apareció publicado con el subtítulo que ya hemos mencionado. En una palabra, este tratado es la primera y después desechada versión del libro tercero de los Principia. Por ello cuando se publicó por primera vez este tratado en Londres en 1728, recién muerto Newton, se publicó con un título casi igual al que llevaba el libro tercero de los Principia; tal título era De Mundi Systemate Liber Isaacci Newtoni. Esta versión fue desechada por Newton porque le pareció que estaba escrita en un lenguaje demasiado llano, «popular» dice él mismo, y por tanto no correspondiente con el tono matemático y muy técnico de los otros dos libros primeros de los Principia. Así que Newton reescribió este libro en lenguaje matemático para los Principia mientras nos dejaba la primera redacción, en lenguaje popular, archivada entre sus papeles hasta después de tu muerte. Más tarde volveremos sobre ello.

En cierto modo podemos decir que con la publicación de los Principia termina la actividad creadora de Newton. Efectivamente, hasta 1727, en que muere, poco más puede decirse de su vida intelectual. En cambio, da paso a su vida pública de hombre ilustre. Ya en 1687 toma parte en la disputa entre la universidad y el rey Jacobo II porque este quería hacer aceptar a un fraile católico como maestro en la universidad. Esto determina que llegue al Parlamento en 1689 por primera vez a donde vuelve después en 1701, como representante ambas veces de la Universidad. No se recuerda que interviniese jamás en la vida parlamentaria salvo para pedir a un conserje que cerrase una ventana. Desde 1690 a 1692 prepara y reúne parte de sus escritos matemáticos y escribe las dos cartas a Wallis en que da noticia de su método de fluxiones y que se publican en 1693. Cae enfermo con una especie de crisis nerviosa o de locura y padece tremendos insomnios y un estado de irritación continua. A principios de 1694 se halla recuperado pero ya no trabaja más en la investigación científica, salvo esporádicamente en la resolución de problemas que circulaban entre los matemáticos de la época como desafíos entre ellos. En 1696 es nombrado, gracias a los buenos oficios de Montague que había sido alumno suyo, Inspector de la Casa de la Moneda (el Mint) y pone todo su empeño en llevar adelante el gran proceso de reacuñación de moneda que se estaba realizando con motivo de la venida al trono inglés de una nueva dinastía.

Desde 1699 es Presidente del Mint con el magnífico sueldo de 1500£ por año y, en consecuencia, en 1701 renuncia a su cátedra Lucasiana de Cambridge. Su vida en Londres se centra en su nuevo trabajo, en la Presidencia de la Royal Society y en sus lecturas y escritos privados. Únicamente vuelve a la vida científica pública para resolver alguno de los problemas matemáticos de la época en cuya resolución deja constancia, una vez más, de su increíble habilidad. Así puede recordarse aquí el problema de Pappo consistente en hallar el lugar geométrico de un punto tal que el rectángulo comprendido entre sus dos distancias a dos líneas rectas esté en una proporción dada al rectángulo comprendido por las distancias a otras dos líneas rectas también dadas. Algunos geómetras de la antigüedad, como Apolonio, intentaron resolver geométricamente la cuestión sin conseguirlo. Para Newton no supuso mayor dificultad demostrar de un modo directo y elegante que dicho lugar es una cónica. Otro desafío célebre fue planteado por J. Bernoulli en 1696, quién escribió a los matemáticos una circular proponiendo a) determinar el brachistocrono, y b) hallar una curva tal que si se traza una línea desde un punto dado O que corte a la curva en P y en Q entonces OP’ + OQ’ sea una constante. Leibniz resolvió la primera parte después de seis meses y sugirió que se le enviase a Newton y a otros matemáticos como una especie de desafío. Newton recibió el problema el 29 de enero de 1697 y al día siguiente devolvió la solución a las dos cuestiones y a la vez dio la solución general para la segunda parte. Y algo parecido volvió a ocurrir en 1716 cuando Newton fue desafiado para que obtuviera la trayectoria ortogonal de una familia de curvas tales como las que describe la Luna al girar a la vez en torno a la Tierra y con esta en torno al Sol. Newton lo resolvió en cinco horas y de paso estableció los principios para hallar las trayectorias.

Si todo lo dicho y mucho más nos lleva a considerar que como matemático y hombre de ciencia su genialidad admite pocas comparaciones en toda la historia, eso mismo pudiera hacernos creer que en Newton solo había preocupaciones científicas, que estas cuestiones y solo estas ocuparon su mente y su vida interior y hasta pudiera parecer demasiado para un solo hombre y una sola vida por larga que fuese. Pero no es este el caso de Sir Isaac. A su muerte dejó una muy cuantiosa colección de manuscritos personales que llegó, con el tiempo, a conocerse con el nombre de «Colección Portsmouth» por ser esta familia —descendientes de Newton— la poseedora de la misma. Cuando los investigadores tuvieron acceso a estos manuscritos hallaron miles de folios escritos por Sir Isaac conteniendo estudios de alquimia, comentarios e interpretaciones de textos bíblicos especialmente los proféticos, así como cálculos herméticos completamente oscuros e ininteligibles para ellos. De esto han tomado pie algunos para relacionar a Newton con sectas herméticas como los Rosacruz, aunque falten en absoluto fundamentos para ello. Posiblemente las cosas vayan en otra dirección muy distinta.

Efectivamente, Newton era un hombre creyente de los llamados fundamentalistas, esto es, de los que creían en la revelación de la Biblia y la entendían al pie de la letra. Además, como Locke, era unitario, es decir, no creía en la Trinidad que consideraba invento papista. Así pues, parece que Newton pensaba que Dios había hecho una segunda revelación en la Biblia en la que completaba la primera hecha en la creación. En esta se halla la ciencia divina expresada en forma de leyes físicas a cuyo conocimiento había llegado Newton por primera vez, con lo que había llegado casi a los mismos confines de la divinidad. Pero aún faltaba mucho por conocer del formidable plan de Dios. El resto de las claves deberían hallarse en la Biblia, la otra «entrega» divina, y por ello Newton acudiría a su estudio de modo tan apasionado. Al menos aquí debería hallarse la clave de la historia —las lucubraciones teológicas y herméticas estarían vinculadas a este intento— entendiendo «historia» como historia total del mundo, de sus elementos astronómicos y de sus elementos humanos también, como partes de un solo plan divino. Newton no se daba por satisfecho con haber logrado desentrañar el complicado sistema mecánico de los astros del sistema solar —y eventualmente de cualquier otro—, sino que creía que eso era solo un subsistema del sistema total, una pequeña parte del enigma —«unas piedras más pulidas o más brillantes halladas en la playa del inmenso océano de la verdad»— y se planteó el desaforado desafío de tratar de alcanzar el fondo del océano, desafío propio de un espíritu titánico y universal. La alquimia, la teología, los estudios y cálculos herméticos debieron ser sus intentos fallidos. Y esto no obstante, nos dan una pista de lo que debió ser el Newton filósofo, metafísico, creyente y hasta un poco renacentista y otro poco medieval. Un Newton que no es la clara y rutilante estrella de la Ilustración, como a veces se ha pensado solo en función de que su «Sistema del Mundo» fuera «el» sistema del mundo de la época ilustrada y fruto de una razón matemática incontaminada. Que sus matemáticas, su física o su óptica hayan ingresado en el templo de la razón y de la ciencia como partes —esenciales— del saber científico de la Ilustración está bien lejos de significar que el hombre que las creó fuese sin más un intelectual de perfiles puros y estereotípicos de la Ilustración. Hay en él algo de medieval y renacentista, cuya mejor expresión se halla en la explícita vinculación teórica a Dios de las cuestiones últimas de la Optica o de los Principia y, en última instancia, de todo el sistema. Esta dependencia del mundo respecto a su Dios —como creador, ordenador, conservador, restaurador, etc.—, no es algo marginal en la filosofía de Newton, sino el punto de convergencia de sus líneas de pensamiento, las cuales se asemejan más al teocentrismo medieval que a la «autonomía del mundo y del individuo» o al «no necesito esa hipótesis», refiriéndose a Dios, de Laplace.

Y volvemos ahora a nuestro tratado. En él Newton expone en un lenguaje asequible —no demasiado matemático— cuatro núcleos principales de temas y algunas otras cuestiones conexas con ellos, relativos a la explicación del sistema de los movimientos de los astros que se mueven en torno al Sol y de las fuerzas y efectos que para ello se requieren y de ello se siguen. En primer lugar el lector encuentra una teoría sobre las relaciones entre cuerpos que se mueven bajo la hipótesis del inverso del cuadrado de las distancias mutuas. De ello se pasa a establecer que la gravedad entre los cuerpos celestes —o lo que sean las fuerzas a las que Newton denomina «gravedad» pero el lector también podría denominar «amor mutuo», por ejemplo— cumple esas leyes de movimiento. Newton por cierto siempre afirmó que desconocía cuál era la naturaleza de eso a lo que denominaba gravedad, aunque mantenía que sus efectos observables o «fenómenos» en los movimientos de los cuerpos daban motivo para creer que era una «fuerza» centrípeta. En este asunto tanto las observaciones de los satélites de Júpiter como de la Luna dan la base empírica sobre la que se alza la generalización, ayudada naturalmente de la hipótesis.

En segundo lugar aborda Newton la descripción de los movimientos de la Luna y de su relación con la Tierra y con el Sol para dar las bases del tema siguiente y dejar echados los fundamentos suficientes de la teoría de la Luna. Hay que hacer notar que los movimientos de la Luna no son de fácil predicción y tampoco Newton estuvo nunca completamente satisfecho de sus cálculos. Sin embargo, su teoría de la Luna es necesaria y en cierto modo suficiente para poder pasar a explicar otro de los grandes problemas a que dio cumplida respuesta Newton como aplicación de su teoría general de la gravitación: Las mareas. Este es un efecto medible y observable de modo tan reiterado como se desee y además grandioso por tu magnitud pues para su producción solo una fuerza de las proporciones de la de la gravedad podría ser adecuada. Por ello, entre otras razones, es tan importante llegar a vincular su explicación a la teoría de la gravitación determinando las magnitudes y relaciones entre ambas. Por eso se detiene Newton en el análisis de los diversos comportamientos de las mareas, de las relaciones con la Luna y el Sol y de los resultados de su acción conjunta o contrapuesta sobre las masas de agua, los tiempos y direcciones de dichas acciones, etc.

La parte final está dedicada a los cometas. En ellos podría verse la excepción a la ley de la gravedad. Por ello Newton aborda la cuestión con dos objetivos: primero, mostrar que tampoco ellos escapan a la ley del universo y, segundo, que, al no escapar, son fenómenos perfectamente naturales, sumisos en todo a la gran ley y por tanto para nada terroríficos o ajenos al sistema. El lector hallará de paso una aplicación a este estudio de los conocimientos ópticos y hasta telescópicos de Newton y, a veces, quedará sorprendido por la finura y sutileza con que logra alcanzar sus resultados.

Este tratado fue en su tiempo uno de los que más contribuyeron a generalizar esta concepción del universo solar que había sido propuesta por Copérnico y perfeccionada por Kepler, aunque solo Newton acabase por dar una formulación completa y suficiente. Como es sabido, este sistema, aún el nuestro en gran medida, fue propuesto por Copérnico y después por Kepler como sustitución del antiguo sistema ptolemaico que era el armazón de la astronomía en la Edad Media y en buena medida del Renacimiento. Pero no fue desplazado de un solo golpe y ofreció grandes resistencias, sobre todo por el hecho de que estaba incorporado a la interpretación del mundo que, en consonancia con ciertas lecturas de la Biblia, había hecho la teología —recuérdese el proceso de Galileo— y era por esto algo así como el sistema astronómico «oficial». Añádase a ello que en el siglo XVII la figura de Descartes como mentor de la filosofía continental había adquirido una notable preponderancia, y en medios científicos y académicos, aunque no precisamente siempre universitarios, primaba su teoría de los Vórtices como explicación mecánica del movimiento de los astros. Finalmente, una creencia alimentada por predicadores de toda índole presentaba a los cometas como fenómenos extraordinarios, «mensajeros de la Cólera Divina», perturbando con ello, más si cabe, el ambiente científico entre los astrónomos. No obstante, para los días de Newton ya se había institucionalizado la observación astronómica y así en 1664, con ocasión del cometa de aquel año, recibieron Boyle, Hooke y otros el encargo de observarlo. Quizá aquí empezó el interés de Newton por ellos, siendo aún estudiante, como sostienen algunos, y desde entonces empezó a reunir datos y a cabilar hasta dar en la primera formulación de 1666. Pero lo cierto es que hasta aproximadamente 1786/87 no redactó el presente tratado y con él la explicación definitiva de los movimientos celestes.

Son tan brillantes las soluciones, tan absolutamente nuevas, tan bien establecidas y tan naturales que la ciencia de la época no tuvo más remedio que rendirse a ellas. En ese proceso cumplió este tratado la misión de vanguardia. Precisamente su carácter «popular» —aunque el lector encontrará que es sumamente riguroso— lo hizo enseguida asequible al público, más y mejor que los Principia de fatigosa y difícil lectura, reservada únicamente a unos pocos matemáticos competentes. En estos medios ya era conocido Newton como matemático e incluso como «mecánico» del universo. Pero de ahí a la aceptación generalizada de su sistema hubo un largo trecho. A recorrerlo ayudó esta obra publicada, en 1728, en Londres casi a la vez que una versión inglesa de la misma (Newton la dejó escrita en latín) y coincidiendo también con la publicación en inglés del Elogio de Fontenelle que en memoria de Newton había leído en la sesión de la Academia de Ciencias de París el 12 de noviembre de 1727. Ambos textos por separado contribuyeron a la fama primero y a la aceptación después —aparte los méritos intrínsecos— de la teoría de la gravitación universal y del modelo de universo que ella venía a explicar. El Continente no tardó mucho en abandonar —al menos los ilustrados y hombres de ciencia— la insostenible teoría cartesiana de los Vórtices.

Hemos hecho la traducción del texto latino tal y como aparece en la edición de las Opera de Newton que hizo Sir Samuel Horsley, ya mencionada, y hemos respetado tanto como hemos podido el estilo conciso y escueto de Newton. Si algo no quedó suficientemente claro no es debido a Newton ni tampoco a que el idioma castellano sea «rebelde y mezquino» para dar cabida a tan altos razonamientos.

El Elogio dará cuenta al lector de la imagen que aquella época tuvo de Newton, y acaso de algunas cosas más. Hoy se dispone de buenas biografías y acaso esa imagen sea distinta porque algo del «iceberg» ha ido aflorando y porque otros aspectos de Newton resultan o no tan grandiosos o algo más humanos. Hemos intentado insinuarlo e invitar al lector curioso a seguir la pista.

Madrid, 2 de marzo de 1983.

E. J. M. Rada